Природные и искусственные материалы для дорожек
Среди большого разнообразия покрытий для дорожек можно выделить три основные группы: твёрдые, мягкие и, так называемые, специальные покрытия.
Твёрдые покрытия, такие как брусчатка, плитка, кирпич, спил, натуральный камень и клинкер, используют на основных дорожках и такие покрытия, как правило, занимают большую часть на участке. Какой материал выбрать зависит в первую очередь от назначения дорожки, от средств, которыми Вы располагаете, ну и конечно, от вкусовых предпочтений. Самым дешёвым и популярным сейчас материалом является брусчатка. Она относительно долговечна, прочна, декоративна и проста в укладке. Плитка хороша своей декоративностью и многообразием цветов и фактур, но недостаточно прочна. Кирпич также со временем трескается и ломается, при укладке кирпичной дорожки, её необходимо фиксировать по бокам (например бордюром из того же кирпича) для более долгой службы.
Мягкие покрытия: галька, мраморная крошка, гравий, опилки (мульча), песок, недавно стали применять такой материал как скорлупа кедрового ореха — она обладает бактерицидными свойствами, обычно применяют на второстепенных дорожках.
К специальным покрытиям относят:
декоративный бетон — он производится уже на месте укладки, толщина такой дорожки может быть разной (от 50 до 200 мм), в зависимости от её назначения. Благодаря использованию красителей, с виду этот бетон может быть как натуральное покрытие, но прочность его не соизмерима. Он устойчив к морозам, к дождям, не скользит и устойчив к агрессивным кислотно-щелочным средам.
Резиновые покрытия — чаще всего используются на игровых или детских площадках.
Они прочные, изготовлены с применением экологически чистых материалов и травмобезопасные. После игры на такой площадке коленки вашего ребенка будут целы.Как выбрать материал для дорожек
Расположение и вид садовых дорожек определяют еще на первоначальном этапе планирования ландшафтного дизайна. Какой материал выбрать, чтобы дорожки были не только красивыми, но и удобными? Посмотрим, какие варианты предлагают ведущие дизайнеры.
Натуральный камень считается одним из самых подходящих материалов для строительства дорожек. К тому же здесь существует столько вариантов фактур, форм и оттенков, что можно не беспокоиться случайно повторить дизайн своего соседа. Для мощения используют более десятка пород камня — как в обработанном (колотом и пиленом), так и в необработанном (плитняк) виде. Фактура тоже варьируется от грубой шероховатой до зеркально-гладкой. Кроме того, из камня можно подобрать любой подходящий для вас цвет. Один только гранит, для примера, занимает спектр от различных оттенков серого до темно-красного и даже черного цвета.
Минус натурального камня в его цене. Самыми дорогими считаются гранит, мрамор, базальт и порфир. Самыми дешевыми — известняк и песчаник. Кроме того, гранит и мрамор зимой покрываются коркой льда и просто превращаются в каток. Поэтому мастера советуют подкладывать под такие украшения сада специальную систему отопления а-ля «теплый пол». Что, разумеется, значительно повышает и так не дешевую стоимость этих дорожек.
Искусственные материалы — бетон, асфальт, бутовый камень и тротуарная плитка. Это наиболее популярные варианты у большинства дачников. Плюсы тротуарной плитки и бетона в том, что они могут запросто имитировать природные материалы — камень или дерево. К тому же плитку всегда можно заказать заранее подходящего вам размера. И еще одно важное свойство — эти материалы весьма устойчивы к перепадам температур. А это уже гарант их долголетия.
Одно из последних новшеств искусственных материалов — тротуарная плитка из пластика. Очень удобна для прокладывания временных дорожек.
И не требует трудоемких работ по установке — она просто втыкается в грунт.
Гравий, галька, щебень, песок — относительно недорогое покрытие. Главное, чтобы камешки были не очень велики. Иначе будет неудобно ходить. По обочинам такой дорожки специалисты советуют все-таки сделать дополнительное укрепление. Например, из ряда уложенных кирпичей или небольших камней.
Кстати, из аналитического обзора, подготовленного специально для нашего сайта, вы можете узнать о динамике цен на песок и щебень.
Дерево. Дорожки из дерева делают обычно в виде поперечных спилов кругляка, заглубленных в землю, или в виде сплошных дощечек. Есть и насыпные деревянные дорожки — из опилок или мульчи.
Главный недостаток этого материала — он быстро раскисает под дождем. А опилки и мульча не рассчитаны на большую нагрузку. При ходьбе насыпь смещается, оседает и быстро теряет свои очертания. Поэтому такие дорожки приходится регулярно подсыпать.
Кирпич — практически идеальный материал для садовых дорожек.
Он крепкий, морозоустойчивый и не выцветает. А кроме того, с помощью геометрии кирпичной кладки можно добиться специального оптического эффекта. Наиболее популярные узоры из кирпича: елочка, плетенка, кирпичик и перпендикулярные ряды.
Трава. Самый трудоемкий и необычный материал для строительства дорожек. Такая трава должна быть устойчива к вытаптыванию и выносить затемнения на тот случай, если дорожка будет проходить по тенистым местам. Строительство такой дорожки ничем не отличается от выращивания настоящего газона.
Если вы не можете выбрать между одним и другим, материал всегда можно комбинировать. Например, можно уложить дорожку из широко расставленной плитки, и засыпать эти расстояния гравием. Камни и дерево хорошо сочетаются с травой. А некоторые дизайнеры советуют выращивать на таких дорожках еще и мелкие яркие цветы.
Садовые дорожки: виды и материалы
Удобно расположенные на участке и надежные дорожки играют очень важную роль в ландшафтном дизайне. При правильном оформлении они являются одной из самых значительных декоративных деталей сада.
При помощи дорожек можно зрительно увеличить площадь участка, разбить его на несколько функциональных зон или, наоборот, соединить между собой несколько разрозненных частей сада. Для того чтобы дорожки правильно использовались и вписывались в общий стиль участка, их расположение необходимо продумать еще на стадии планирования сада. При этом следует учитывать множество факторов — наиболее живописные места участка, расположение мест отдыха и хозяйственных построек. В зависимости от назначения необходимо рассчитать ширину дорожки. Главная дорога, ведущая к дому, должна быть достаточно широкой, лучше всего мощенной. Ширина ее составляет от 180 см. до 2 м.
Роль садовых дорожек в ландшафтном дизайне
Если главная дорожка предназначена для въезда автомобиля, то ее следует делать шире. Основные, часто используемые дорожки должны быть шириной 150-180 см., чтобы по ним одновременно могли проходить два человека. В отдаленные и мало посещаемые места участка можно проложить узкие дорожки или тропинки шириной 40-80 см.
Поверхность дорожки должна удовлетворять трем основным критериям: она должна хорошо выглядеть; быть прочной и долговечной; сравнительно легко приводиться в порядок и содержаться в хорошем состоянии. В качестве материалов, наилучшим образом удовлетворяющих этим условиям, можно указать следующие: бетон; различные виды плит и блоков для дорожного покрытия, уложенные либо свободно, либо на растворную постель; щебень и, наконец, асфальт. Каждый из них имеет свои достоинства и недостатки.
Покрытие для дорожек следует выбирать в зависимости от рельефа и дизайна территории. Для садов в деревенском стиле прекрасно подойдут дорожки из камня, дерева, клинкерного кирпича; дорожки в классических загородных садах можно покрыть небольшими бетонными плитами или посыпать гравием. Покрытие дорожек также зависит от их назначения. Например, на парадную дорожку следует обратить особое внимание, так как она является визитной карточкой участка и дома.
Покрытие главной дорожки должно быть прежде всего красивым. Покрытие основных дорожек делают более прочными, так как нагрузка на него выше. Лучше всего использовать для этих дорожек камень, асфальт или вмурованную в раствор гальку. Для покрытия второстепенных дорожек можно использовать асфальт, бетон или бутовый камень. Мало используемые и отдаленные тропинки лучше всего оставить без покрытия.
Разновидности садовых дорожек
Дорожки из дерева
Одним из распространенных материалов для покрытия дорожек является дерево, которое используется в нескольких видах: чурбачки, утопленные в землю, доски или опилки (для насыпных дорожек). Деревянное покрытие хорошо тем, что создает ощущение тепла, однако дорожки из дерева очень страдают от сырости. Покрытие из опилок очень красиво выглядит, однако по нему не слишком удобно ходить. Чтобы деревянное покрытие прослужило дольше, его следует укладывать на открытые и освещенные места, где оно будет меньше подвергаться воздействию влаги.
Для насыпных дорожек наиболее подходящими материалами являются гравий, песок, галька и щебень. При использовании этих материалов необходимо следить, чтобы камни не были слишком крупными, так как по ним будет неудобно ходить. Насыпные дорожки рекомендуется укреплять по бокам каким-либо бордюром, чтобы покрытие не рассыпалось и не теряло формы.
Дорожки из натурального камня
Натуральный камень представляет собой оптимальный вариант покрытия. Он бывает как в виде плит, так и в виде необработанных булыжников различного цвета и фактуры. К наиболее дорогим видам камня относятся мрамор, базальт и гранит, которые придают дорожкам элегантный и торжественный вид.
В холодное время года эти виды камня неудобны в использовании, так как покрываются льдом. Чтобы избежать этого под полотном дорожки можно установить систему обогрева. Более дешевые виды камня — такие, как песчаник и известняк, — не требуют особого ухода и долговечны в использовании.
Насыпные дорожки
Для насыпных дорожек наиболее подходящими материалами являются гравий, песок, галька и щебень.
При использовании этих материалов необходимо следить, чтобы камни не были слишком крупными, так как по ним будет неудобно ходить. Дорожки необходимо тщательно утрамбовать ручными или автоматическими трамбовками. При устройстве любых, в том числе и насыпных дорожек учитывают рельеф, ландшафтный дизайн сада и архитектурный стиль дома. Насыпные покрытия делают в случае, если они не будут нести значительных нагрузок. Главное достоинство насыпных дорожек — они могут быть декоративными и хорошо вписываться в общий ландшафт и на них не застаивается вода.
Насыпные дорожки рекомендуется укреплять по бокам каким-либо бордюром, чтобы покрытие не рассыпалось и не теряло формы.
Дорожки из искусственных материалов
На протяжении долгого времени большой популярностью пользуются покрытия из искусственных материалов: бетона, бутового камня, асфальта и тротуарной плитки. Чаще всего из этих материалов используется бетон, который отличается высокой прочностью. К тому же в последнее время появился декоративный бетон, имитирующий каменную кладку.
Тротуарная плитка бывает бетонной и пластиковой. Бетонная плитка довольно часто используется для покрытия садовых дорожек. Одним из ее главных достоинств является разнообразие форм расцветок и толщины. Встречается также плитка с рисунком, имитирующим природный камень.
Пластиковая плитка также очень красива и удобна. Главное достоинство этого покрытия заключается в простоте применения: плитку не нужно закреплять раствором, ее укладывают прямо на грунт.
Дорожки из кирпича
Клинкерный, или пережженный кирпич отличается почти такой прочностью и долговечностью, как и камень. Он не подвержен воздействию влаги, долго сохраняет цвет. Из этого кирпича можно выкладывать как дорожки, так и бордюры. Покрытие из кирпича привлекательно прежде всего тем, что его можно укладывать различными способами: елочкой, поперечными или продольными рядами, плетенкой или кирпичиком.
Вышеперечисленные материалы можно использовать и в различных комбинациях: например, бетонные плиты уложить на некотором расстоянии друг от друга, а промежутки засыпать гравием или кирпичную дорожку выложить по бокам камнем.
Для того чтобы дорожки дольше служили и сохраняли свои внешние качества, при укладке следует обращать внимание на несколько факторов. Во-первых, покрытие, вне зависимости от вида, должно быть качественным; во-вторых, необходимо знать особенности каждого материала и его использования.
Дорожки являются жизненно важным элементом всей композиции сада. По ним можно прогуливаться, кататься на велосипеде. Они придают саду индивидуальность. А материал, из которого они сделаны, влияют на впечатление, производимое садом.
Материалы для дорожек
Каждый владелец загородного дома желает о том, чтобы его участок был не только практичным и удобным, но и красивым.
Отличным средством для одновременного удовлетворения данной потребности является монтаж садовой дорожки. Как правило, небольшие тропинки появляются самостоятельно, но они не только не вписываются в дизайн участка, но и трудны в использовании в сырую погоду. В настоящее время существует огромное количество материалов, используемых для укладки садовой дорожки. В первую очередь специалисты рекомендуют использовать тот материал, из которого построен дом – они будут прекрасно сочетаться, создавая красивое дизайнерское решение. Но, все же, следует ознакомиться с перечнем материалов для садовой дорожки, которые в настоящее время пользуются колоссальным спросом среди владельцев загородных домов.
Натуральный камень для дорожек
Многие ландшафтные дизайнеры считают натуральный камень колоритным и благородным материалом, который способен лаконично вписаться в совершенно любое дизайнерское решение. Но, в связи с высокой стоимостью расходного материала, такие дорожки встречаются не так уж и часто.
Люди с высоким бюджетом могут использовать для монтажа садовой дорожки базальт или гранит, мрамор или порфир. Более доступными натуральными камнями являются песчаник и известняк. Все они отличаются своим собственным цветом. Помимо этого, специалисты говорят о том, что в некоторых случаях можно использовать необработанный камень, собрать который можно в гористой местности. Также зачастую используется пиленый камень, который по своей форме максимально схож с плиткой, о которой мы подробно поговорим ниже.
К достоинствам такого материала для садовой дорожки можно отнести тот факт, что он способен прослужить достаточно большое количество времени. Помимо этого, натуральный камень – это экологически чистый продукт, причем весьма привлекательного внешнего вида, который придаст приусадебного участку еще больше индивидуальности и эстетичности.
Но не стоит забывать о некоторых недостатках подобного материала:
- В связи с тем, что камни достаточно много весят, самостоятельно монтировать такую дорожку весьма затруднительно с физической стороны.
- Натуральный камень – не дешевое удовольствие, которое по карману далеко не каждому.
- В зимний период камень может покрыться льдом, тем самым образовывая опасность получения серьезной травмы.
Натуральный камень для мощения
Читайте также: Планировка дорожек в саду
Тротуарная плитка для дорожек
Тротуарная плитка в последнее время пользуется популярностью среди дачников, решивших смонтировать садовую дорожку. Это и не удивительно, ведь данный материал, помимо достаточно высоких технических характеристик, дает возможность создать какой-угодно узор на садовой дорожке.
Однако при выборе материала следует учитывать достаточно большое количество нюансов, чтобы заполучить качественный товар, а не подделку. Поговорим о некоторых советах, к которым лучше всего прислушаться при выборе тротуарной плитки для дорожки:
- Материал, из которого изготовлена плитка, имеет огромное значение. Следует обратить внимание на состав раствора, из которого изготовлена плитка, а также на то, по какой технологии она произведена. Эту информацию должны предоставить в магазине, так как она не является закрытой от потребителя. Также можно попросить сертификаты качества и соответствия материалов и готового товара.
Эту информацию должны предоставить в магазине, так как она не является закрытой от потребителя. Также можно попросить сертификаты качества и соответствия материалов и готового товара.- Толщина плитки также имеет огромное значение. Для пешеходных дорожек лучше всего использовать плитку, толщина которой не менее 3 сантиметров. Лучше всего выбирать плитку небольшого размера, так как среди специалистов бытует мнение, что чем меньше размер плитки – тем она прочнее и надежнее.
- Особое внимание следует обратить на внешний вид плитки. Гладкость и яркость плитки – не всегда залог качества! В качестве проверки прочности материала, возьмите две плитки и ударьте их друг о друга – в том случае, если звук звонкий – материал прочный, если глухой – то он перенасыщен добавками и водой и внутри него большое количество пор.
тротуарная плитка
Читайте также: Деревянные дорожки для дачи
Садовая дорожка из георешетки
Георешетка – это одно из новшеств, которое стало использоваться в ландшафтном дизайне относительно недавно.
Но уже, несмотря на свое «возраст», данный материал для укладки садовой дорожки пользуется спросом среди владельцев загородных домов и дач. Это и не удивительно, ведь для монтажа необходима только лишь георешетка необходимой зернистости и щебень или мелкий гравий.
В настоящее время производители готовы предложить два основных типа георешетки: из твердого полимерного пластика или из гибкой полимерной ленты, крепленной в специальные модули. Что касается первого типа, то он просто устанавливается в качестве садовой дорожки. Со вторым типом все сложнее: их необходимо растянуть и закрепить при помощи колышков в почве.
Георешетка может иметь различную высоту и ячейки разного размера. Делать выбор необходимо, отталкиваясь от того, какого размера гравий или щебень планируется использовать. Все равно, заполненная решетка не будет видна, после того, как она будет заполнена материалом.
георешетка
Читайте также Дорожка из спилов дерева
Лучшие материалы для садовой дорожки
Садовую дорожку несложно замостить обычным кирпичом или залить бетоном.
Но так поступить проще всего. Настоящие эстеты не ищут легких путей, поэтому используют самые современные стройматериалы для оформления своей загородной резиденции. Итак, какие же покрытия для дачных дорожек нынче в моде?
Ковер из камней
Самым классическим и вместе с тем трудоемким вариантом является мозаика из природного камня. Причудливые узоры и орнаменты идеально впишутся в любой ландшафт. Немного «состарив» такую дорожку, вы получите мотивы традиционного английского сада. Здесь все зависит исключительно от вашего времени, ведь чем дольше вы будете возиться, выкладывая оригинальные рисунки, тем красивее у вас получится.
Беговая дорожка
Дорожка из ярких резиновых плит или резиновой крошки идеально впишется в лаконичное оформление вашей дачи. За таким покрытием легко ухаживать, его удобно устанавливать/демонтировать. Резиновые дорожки имеют ярко выраженную спортивную внешность. А если на них нанести еще и разметку, то они будут выглядеть и вовсе как на стадионе.
Каменная кладка из гладких плит
Дорожки, оформленные массивными каменными плитами, создают ощущение средневековой Европы. Особенно необычно такие тропинки будут смотреться среди грядок и зарослей фруктовых деревьев. Как вариации используют известняк или плитняк. Однако в моде среди современных дачников – искусственный камень. Его особенность в том, что он может повторять текстуру любого природного камня. Плиты из такого материала могут быть самой разной формы ‒ ромбовидными, волнистыми, круглыми и т.д. Камень, имитирующий текстуру дерева, особо выигрышно смотрится, если ваш ландшафт стилизован под старину.
Боскеты Версаля
Еще недавно непозволительной роскошью считалась садовая дорожка, выполненная из паркетной доски. Сейчас этот материал называется «декинг». Стоит сказать, что дерево в качестве дорожного покрытия использовалось всегда, к тому же оно смотрится очень привлекательно на фоне пробивающейся между щелей травы.
Единственный существенный недостаток дерева заключается в том, что оно гниет под действием влаги. Однако современные древесно-полимерные композиты не боятся ничего и выглядят привлекательно довольно продолжительное время. Садовая дорожка из дерева будет прекрасным продолжением любого загородного дома.
Материалы по теме
Какие материалы используют для мощения дорожек и тротуаров
Вступление
Для того чтобы преобразить приусадебную дорожку, достаточно правильно и грамотно оформить дорожки. Для этого потребуется использовать качественные и прочные материалы, которые по истечении долгого времени не изменят своих изначальных характеристик.
В сегодняшней статье мы с вами поговорим о наиболее популярных и широко востребованных материалах, которые в последнее время все чаще используются для мощения тротуаров и тропинок.
Материалы для мощения дорожек и тротуаров
Прежде чем отдавать предпочтение определенному сырью, потребуется предварительно разобраться с особенностями рельефа и дизайна придомовой территории. Кроме этого важно учитывать характеристики самих стройматериалов.
Натуральный камень
Конечно же, натуральный камень является достаточно колоритным и благородным сырьем, способным идеально вписаться в любой экстерьер. Однако он не так уж и часто используется для укладки садовых дорожек ввиду своей высокой стоимости. При этом важно отметить, что натуральный камень может иметь разный цветовой оттенок, что в свою очередь позволяет подобрать его к определенному ландшафту.
К основным преимуществам данного строительного помощника можно отнести длительный эксплуатационный период, абсолютную экологичность и привлекательность.
А вот среди недостатков присутствует чрезмерный вес, высокая стоимость и возможность обледенения.
Для мощения дорожек и тротуаров брусчатка
Брусчатка также зачастую используется для тротуаров. Она намного качественнее и надежней асфальта. Именно поэтому тротуарная плитка нашла своей применение при обустройстве садовых тропинок и дорог.
На современном рынке строительных материалов представлен большой выбор брусчатки от разных производителей и в разном цветовом ассортименте. Именно поэтому каждый владелец может подобрать для собственной территории наиболее подходящую по всем критериям плитку.
Среди основных достоинств брусчатки присутствует простота монтажа, привлекательный вид, а также высочайший уровень прочности. К тому же тротуарная плитка способна великолепно функционировать в широком диапазоне рабочих температур, чрезмерных нагрузках и повышенной влажности.
Кирпич
Также в последнее время строители стали использовать для мощения дорожек и тротуаров традиционный кирпич.
Данный материал представлен в различных цветовых оттенках, что в свою очередь позволяет создавать с его помощью оригинальные композиции.
К основным преимуществам кирпича можно отнести привлекательность, высочайшую прочность и долговечность.
Бетон
Конечно же, в этом деле можно также использовать бетон. Это, наверное, один из наиболее надежных стройматериалов, который не теряет своих характеристик на протяжении долгого времени. Кроме этого он является достаточно прочным, влагоустойчивым, термостойким и легким в укладке сырьем.
Еще статьи
Похожие записиМатериалы для обустройства садовых дорожек
Если у вас есть сад, то обязательно перед вами встанет вопрос об обустройстве садовых дорожек. Их выполняют из различных материалов, в соответствии с предпочтениями и финансовыми возможностями, а также исходя из тех функций, для которых они предназначены.
Самым надежным и простым материалом для садовых дорожек является кирпич, поскольку он достаточно прочен, морозоустойчив, и не требует особого ухода.
Также очень распространены дорожки из асфальта, бетона или тротуарной плитки. Такие материалы также достаточно прочны и долговечны.
Многие при устройстве дорожек применяют гравий, песок, щебень и гальку, а также их смеси в разных соотношениях. Однако в данном случае важно, чтобы камешки не были очень большими, так как ходить по такой дорожке в дальнейшем будет неудобно. Следует заметить, что эти материалы не слишком дорогие, и обустройство таких садовых дорожек не потребует больших денежных вложений. Но если вы решились использовать именно такие материалы, то придется делать укрепление по бокам дорожки, чтобы избежать ее дальнейшего размывания и рассыпания по краям.
Можно на небольших дачных участках сделать насыпные дорожки из опилок и мульчи, а также из деревянных досок или кругляка. Это обойдется совсем дешево, однако прослужат такие материалы тоже недолго, поскольку дерево и опилки быстро раскисают от влаги. Поэтому дорожки придется время от времени подсыпать свежими опилками.
Мраморная плитка в обустройстве садовых дорожек
Очень красиво смотрятся дорожки в саду, оформленные натуральным или искусственным камнем. Тут, конечно, будет небольшая разница в цене, однако сад при этом будет выглядеть неотразимо. Существует огромный выбор натурального камня с различной фактурой и цветовыми оттенками. Наиболее популярным материалом при обустройстве садовых дорожек является мрамор. Мраморная плитка придает неповторимый вид Вашему саду, а практичность использования этого натурального камня — заставит Вас задуматься над вопросом: «Может лучше немного доплатить, но взять натуральный мрамор?».
Поверхность камня может быть как шероховатой, так и зеркальной. Но камень в зимний период будет покрываться ледяной коркой. Об этом следует помнить, чтобы при устройстве таких дорожек заранее спроектировать и проложить систему для их подогрева. Наиболее дорогими считаются гранит и мрамор, а более дешевыми камнями — известняк и песчаник.
Среди новейших современных материалов наиболее популярна плитка из пластика.
Эта тротуарная пластиковая плитка достаточно прочна, долговечна, надежна, ее легко укладывать в грунт. Она также не требует огромных затрат, не требует особого ухода, и выпускается в различных вариациях.
Долговременная прочность пористых геоматериалов с помощью микромеханической модели с учетом чередующихся условий смачивания и высыхания
Данное исследование посвящено определению долговременной прочности пористых геоматериалов в условиях чередующегося смачивания и высыхания с помощью анализа статической приспособляемости. В рамках микромеханики пористых материалов модель полой сферы Гурсона с твердой матрицей Друкера-Прагера принята в качестве репрезентативного элемента объема. Эффекты попеременного смачивания и высыхания рассматриваются как переменное давление воды, воздействующее на внутреннюю граничную поверхность элементарной ячейки.Циклические отклики разделены на чистую гидростатическую часть при сжимающих/растяжающих нагрузках и дополнительную девиаторную часть для захвата эффектов сдвига.
Снижение длительной прочности из-за внутреннего давления воды наблюдается на иллюстрации полученных макроскопических критериев по отношению к различным параметрам нагрузки. Кроме того, точность аналитического решения также проверяется путем сравнения с результатами пошаговых расчетов на основе МКЭ.
1. Введение
Переменные нагрузки широко распространены в инженерных сооружениях, таких как откосы, фундаменты морских платформ и тротуары [1–3].Долговременная прочность геоматериалов в этом состоянии заметно снижается по сравнению с тем, что подвергается постоянной нагрузке. Действительно, экспериментальные наблюдения [4–6] и численное моделирование [7, 8] уже показали, что деформации разрушения при циклических нагрузках значительно ниже, чем достигаемые монотонным путем.
Кроме того, учитывая почву или горные породы над уровнем воды в подземных сооружениях, попеременное увлажнение и высыхание из-за колебаний уровня воды еще более вредно для ее долговременной стабильности, что является обычным случаем в естественных условиях.
условие [9].Следовательно, прочность геоматериалов, полученных в случае пропорционального или постоянного нагружения, соответственно снижается из-за переменных нагрузок и чередующихся условий смачивания. С этой целью анализ приспособляемости, мощный инструмент для предоставления важной информации о материале при циклических нагрузках в предельном состоянии, принят в этом исследовании для расчета снижения прочности.
Два двойных теоретических подхода к приспособляемости были представлены в этой теме. Статический был впервые разработан Меланом [10].Он утверждает, что конструкция разрушается, если можно найти так называемое не зависящее от времени поле остаточных напряжений, такое, что условие текучести всегда выполняется во всем теле. Статический подход получил широкое распространение и развитие в технике [11–13] теоретически и численно, поскольку получаемая предельная нагрузка строго ниже реальной. С другой стороны, кинематический подход основан на ключевом понятии допустимого приращения пластической деформации, впервые введенном Койтером [14] и развитом в [15–17].
В частности, расширение Кёнигом и Семашко [18] теоремы Мелана позволяет проверить условие приспособляемости с помощью критических циклических нагрузок, содержащих все вершины в области нагрузки, вместо любого произвольного пути нагрузки.
Учитывая тот факт, что большинство геоматериалов содержат микроструктуры [19, 20] (поры, минеральные включения и т. д.), которые вызывают неупругое макроскопическое поведение, многочисленные работы были посвящены изучению влияния микроструктуры на геоматериалы в рамках микромеханики. [21–25], особенно пор [26, 27].Используя модель полой сферы Гурсона [28], тензоры напряжений раскладываются как сумма чистой гидростатической части при сжимающих/растяжающих нагрузках и дополнительной девиаторной части для учета эффектов сдвига [29–31] благодаря симметричной геометрии. Первый автор уже применил теорему статической приспособляемости для определения предельной нагрузки пористых материалов [32–34] с этой моделью, подвергаемой 1 независимой циклической нагрузке.
В этой работе условия нагружения еще более сложные, чем в упомянутых работах.Гидростатическая и девиаторная части нагрузки больше не связаны трехосностью наложенного макроскопического напряжения. Другими словами, в настоящем исследовании рассматриваются две независимые нагрузки, для которых в литературе имеются только численные решения [35]. Кроме того, условия попеременного увлажнения и высыхания моделируются переменным давлением воды, приложенным к внутренней граничной поверхности модели полой сферы. Считается, что твердая матрица подчиняется закону текучести Друкера-Прагера, чтобы описать пластическую сжимаемость и асимметричное поведение между растяжением и сжатием геоматериалов на макроуровне.Ожидается, что полученный макроскопический критерий гомогенизации позволит прогнозировать длительную прочность пористых геоматериалов в условиях попеременного увлажнения и высыхания.
Статья организована следующим образом. В разделе 2 кратко напоминаются формулировки, основанные на микромеханике, и теорема о статической приспособляемости.
Приведен также критерий макроскопической прочности пористых геоматериалов, основанный на предельном анализе, предложенный в [29]. Снижение прочности из-за переменных нагрузок с учетом чередующихся условий смачивания и высыхания, указанное макроскопическим критерием приспособляемости, приведено в разделе 3.Первый и второй подразделы посвящены микроскопическим полям напряжений и применению статической теоремы, а в третьем подразделе учитывается переменное давление воды. В разделе 4 выполняются пошаговые упругопластические численные расчеты для различных вариантов нагружения, и результаты сравниваются с полученным аналитическим решением. Выводы и перспективы приведены в последнем разделе.
2. Микромеханическая модель и гомогенизированный макроскопический критерий для пористых геоматериалов
В этом разделе впервые представлен основанный на микромеханике репрезентативный объемный элемент полой сферы (RVE) пористых геоматериалов.Используя эту модель, мы напоминаем также критерий макроскопической прочности, предложенный Guo et al.
[29], которые могут описать пластическую сжимаемость и асимметричное поведение между растяжением и сжатием исследуемых материалов на макроуровне.
2.1. Гомогенизация пористых геоматериалов и модель полых сфер
Мы рассматриваем класс пористых геоматериалов, характеризующихся твердой фазой и порами на микроуровне, в которые встроены поры (см. рис. 1). Классическая модель полой сферы Гурсона [28] с граничным условием равномерной скорости деформации используется для изучения макроскопического поведения этого типа материала путем гомогенизации.
Внутренний и внешний радиусы выбранной полой сферы RVE соответственно обозначены как и . Обозначим общий объем РПО, тогда как объем пустот. Таким образом, объемная доля пустот определяется выражением . Граничное условие равномерной скорости деформации задается на внешней поверхности полой сферы, где – равномерная макроскопическая скорость деформации и вектор положения. Твердая матрица упругопластична и считается, что в этой работе она подчиняется связанному с ней пластическому закону Друкера-Прагера (без учета эффектов упрочнения), чтобы продемонстрировать асимметрию растяжения-сжатия геоматериалов:
где – эквивалентное напряжение, определяемое девиаторной частью тензора напряжений, – среднее напряжение.
представляет собой предел текучести матричного материала и коэффициент чувствительности к давлению, связанный с углом трения:
Имея микроскопические поля напряжений и скоростей пластических деформаций соответствующие макроскопические значения ЭПР можно рассчитать как средние значения [36]:
Более того, поле макроскопических напряжений можно просто получить интегрированием по поверхности, а не по объему: если микроскопический статически допустим в котором — единичный вектор нормали наружу к элементарной ячейке.
Согласно лемме Хилла для допустимых полей с учетом граничного условия равномерной скорости деформации всегда выполняется следующее равенство, связывающее диссипацию на микро- и макромасштабах:
2.2. Критерий макроскопической прочности
В рамках предельного анализа критерий макроскопической прочности пористых геоматериалов может быть получен из критерия микроскопической пластической текучести матрицы:
описывающее нелинейное пластическое поведение гомогенизированных пористых геоматериалов.
Кроме того, могут быть отражены эффекты объемной доли пустот. Точность гомогенизированного критерия зависит главным образом от приложенных полей напряжения и скорости деформации полой сферы на микроуровне. В этом подразделе мы представляем гомогенизированную континуальную модель, построенную вокруг трехпараметрического осесимметричного поля скоростей [29] Guo et al.
В цилиндрической системе координат в ортонормированной системе координат принимается следующее трехпараметрическое поле скоростей: где для . , , и – параметры.
Рост пустот можно рассчитать как в котором , а знак представляет рост пустоты () или сжатие ().
С помощью методов предельного анализа предлагается следующий неявный макроскопический критерий пористых геоматериалов, состоящих из твердой матрицы Друкера-Прагера: где и соответственно могут быть выражены гипергеометрической функцией Гаусса с символами Поххаммера и парой отношений , .
Заметив, что инварианты макроскопического тензора напряжений могут быть получены аналогично их микроскопическим аналогам,
— девиаторная часть .
Гомогенизированные критерии текучести Го, в основном определяемые уравнением (10) для пористых геоматериалов, представлены на рисунке 2 в зависимости от различных значений пористости (красная линия: , зеленая линия: и синяя линия: ). На этом же рисунке представлен и классический критерий текучести Друкера-Прагера (чёрный штрихпунктир), в котором не учитывается влияние пористости геоматериалов (). Интересно отметить, что объемная доля пустот оказывает большое влияние на поверхность текучести замкнутой формы, что обеспечивается макроскопическим критерием (10).
В отличие от феноменологического закона текучести (например, модели Друкера-Прагера), эта модель, основанная на микромеханике, может отражать дилатантное и сжимающее поведение геоматериалов в испытании на трехосное сжатие. Например, в области низкого всестороннего давления () легко наблюдается пластическая дилатансия геоматериалов, тогда как при высоком всестороннем давлении может быть получена контрактность ().
Даже для одних и тех же условий нагрузки дилатантные и контрактантные явления различны из-за влияния пористости.Под ограничивающим давлением он находится в дилатантной области для и в сжимающей области для вместо этого. Кроме того, согласно критерию Гуо, также наблюдается асимметричное поведение геоматериалов при сжатии/растяжении и снижение прочности на макроуровне из-за пор. Более подробный вывод вышеуказанного макроскопического критерия см. в [29].
3. Снижение прочности из-за переменных нагрузок с учетом чередующихся условий смачивания и высыхания
Этот раздел посвящен расчету снижения прочности пористых геоматериалов, подверженных переменным нагрузкам, по сравнению с гомогенизированным критерием текучести (уравнение (10)).Как упоминалось в первом разделе, эффективная несущая способность материалов также зависит от различной амплитуды приложенных нагрузок. Как и в пионерских теоретических работах [32, 34, 37] по пористым средам, поля напряжений и деформаций полой сферы RVE разделены на гидростатическую и девиаторную части с учетом осесимметричной геометрии.
Следует отметить, что, в отличие от предыдущих исследований, где переменные нагрузки задаются пропорциональными в течение каждого цикла (являются постоянными), гидростатические части и считаются в статье независимыми с целью сохранения общности инженерных задач.Другими словами, долговременная стабильность пористых геоматериалов касается многомерной проблемы приспособляемости, а не одной. Если нагрузка изменяется в некоторой области, для которой после переходной фазы отклик материала становится линейно-упругим (приспособляемость). Это обеспечит долгосрочную сохранность пористых геоматериалов.
3.1. Преобразованная задача о переменной нагрузке и теорема о статической приспособляемости
Учитывая приложенную переменную нагрузку в области (см. рис. 3(а)), остаточные напряжения в рассматриваемой модели могут быть получены путем вычитания упругих откликов из полных напряжений: где – чисто упругие реакции на напряжения в фиктивной упругой ячейке.
(a) Исходная переменная нагрузка
(b) Эквивалентные циклы нагрузки
(a) Исходная переменная нагрузка
(b) Эквивалентные циклы нагрузки
Согласно классической теореме приспособляемости Мелана [1].
если существует не зависящее от времени поле остаточных напряжений такое, что
выполняется в любом месте тела в любое время, материал встряхивается. представляет собой функцию текучести твердой матрицы (уравнение (1)). Тогда рассеиваемая энергия ограничена во времени, независимо от начального состояния.
Более того, не зависящее от времени поле остаточных напряжений в ключевой точке принадлежит к набору статически допустимых полей (уравнение (5)) в настоящем исследовании:
Благодаря уравнению (4) поверхностное интегрирование налагает следующее особое соотношение, связывающее остаточные напряжения на макро- и микромасштабах: такие, что средние остаточные напряжения равны нулю и идентичны макроскопическим упругим напряжениям в фиктивном упругом теле:
Давайте введем коэффициент нагрузки, который контролирует размер фактической области нагрузки.За порогом максимально допустимой нагрузки тело не может находиться в состоянии приспособляемости при переменных нагрузках.
В результате найти предельный коэффициент нагрузки при приспособляемости , за пределами которого происходит разрушение вследствие усталости или образования механизма (постепенное обрушение на первом цикле), является основной задачей данной статьи для обеспечения долговременной устойчивости пористых геоматериалов.
На практике состояние приспособляемости при исходной произвольной нагрузке, гарантированное теоремой Мелана, может быть преобразовано согласно Кёнигу и Семашко [18]: если данная конструкция притрясается по любому пути нагружения, содержащемуся в данной области нагрузки , то она также притрясается по любому пути нагрузки, содержащемуся в выпуклой оболочке .Другими словами, условие приспособляемости необходимо проверять только на пути циклической нагрузки, содержащем все вершины области гипермногогранной нагрузки (например, на рис. 3(b), путь 1 ⟶ 2 ⟶ 3 ⟶ 4 ⟶ 1), а не любой произвольный путь загрузки в пределах одного домена. Это также называется теоремой о выпуклой оболочке.
Учитывая понятие коэффициента нагрузки, фактическую нагрузку можно разложить на комбинацию нескольких элементарных где — тот же коэффициент, определенный в и эталонных нагрузках.Множители нагрузки независимы в диапазоне . В этом исследовании количество независимых нагрузок . Следовательно, две элементарные нагрузки образуют двумерную выпуклую область нагрузки, имеющую 4 вершины.
3.2. Макроскопический критерий приспособляемости пористых геоматериалов при переменных нагрузках
Вспоминая предыдущие исследования по анализу приспособляемости пористых сред при одной циклической нагрузке, пробные поля напряжений на микроуровне разделены на две части:
для описания эффектов сжатия/растяжения и сдвига модели полой сферы, подвергаемой чисто гидростатическим и девиаторным нагрузкам соответственно.Следует отметить, что построение пробных полей напряжений уже предусмотрено в предыдущем исследовании [34]. Чтобы не повторяться, в следующих частях мы приводим только выражения этих полей.
(1) Как указано в уравнении (13), точное поле напряжений под действием гидростатической нагрузки рассматривается как сумма двух частей:
Поле упругих напряжений в фиктивном теле задается в сферических координатах:
Соответствующее поле остаточных напряжений записывается следующим образом: (2) Аналогично, дополнительные члены поля напряжений при девиаторной нагрузке есть где фиктивное поле упругих напряжений записывается как с коэффициентом Пуассона и третьим инвариантом макроскопического девиатора напряжений.
И соответствующий остаток принимает вид , где максимальное значение и связано с где – константа, подлежащая определению, и – функция от , учитывая, что подробный вывод впервые приведен в [33].
Следовательно, было получено полное выражение полных микроскопических полей напряжений (19). Вдохновляясь предыдущими исследованиями [32, 34], наиболее «опасная» точка рассматриваемой модели полой сферы всегда находится на внутренней границе ().В этом случае среднее напряжение и эквивалентное напряжение можно легко вычислить из уравнения (19) в уравнение (25): где (соответственно, ) — максимальное значение (соответственно, минимальное значение) третьего инварианта в девиаторном пространстве, а
Согласно статической теореме Кенига и Семашко [18], только критические пути циклического нагружения, содержащие все вершины области нагрузки (рис.
3(b)) должны быть проверены, чтобы гарантировать безопасность материала. В данном исследовании приложенные нагрузки считаются изменяющимися от нуля до максимального значения:
что является наиболее распространенным случаем в технике.Как показано на рисунке 4, существуют пути загрузки 1, 2 и 3, включающие 4 вершины: , , , и .
Комбинируя условие приспособляемости (14) и микроскопическое поле напряжений (20), можно получить следующие уравнения в вершинах в предельном состоянии приспособляемости (достигается равенство):
Введем трехосность общего напряжения с учетом чисто упругих откликов в области нагрузочной способности приспособляемости, которая определяется выражением для подключения пути нагрузки и . Аналогично, для вершин и имеет место следующее соотношение:
Ссылаясь на [34], можно исключить, применив уравнение (34) к первым двум условиям приспособляемости (30) и (31).Решая два уравнения относительно знака , можно получить
Принимая во внимание трехосность общего напряжения (34), макроскопический критерий приспособляемости пористых геоматериалов, полученный из уравнений (30) и (31), равен
Аналогичным образом, в результате двух последних условий приспособляемости (32), уравнения (33) и общей трехосности напряжений (35) другая часть для выполнения полного макроскопического критерия приспособляемости равна
Согласно предыдущим исследованиям, наиболее «опасная точка» принятой модели полой сферы находится на экваторе () или полюсах ( или ) в зависимости от знака , где
Установленный макроскопический критерий приспособляемости (уравнения (37) и (38)) проиллюстрирован на рисунке 5 пористостью и коэффициентом Пуассона .
Угол трения твердой матрицы принимается равным 30°. Предельные поверхности, определяемые предложенным макроскопическим критерием, нанесены штрихпунктирной линией (зеленая линия для коллапса на экваторе, синяя линия для коллапса на полюсах). В результате эффективная область приспособляемости ограничена красной сплошной линией.
По сравнению с аналитическим исследованием пористых сред при одной независимой нагрузке полученная область приспособляемости на рис. 5 полностью симметрична относительно оси .Его можно рассматривать как «случай пульсирующего нагружения» в [34], но гидростатическая часть не связана с девиаторной частью через трехосность напряжения. При этом явно видно, что знак не влияет на конечную область приспособляемости (красная линия). Действительно, этот интересный вывод согласуется с численным исследованием [35] по нелинейной оптимизации на основе метода внутренних точек, которое касается анализа приспособляемости пористых сред, имеющих твердую матрицу фон Мизеса.
3.3. Долговременная стабильность в условиях попеременного увлажнения и высыхания
Как упоминалось в первом разделе, условия попеременного увлажнения и высыхания возникают в некоторых геоинженерных конструкциях и снижают их долговременную прочность. Очевидно, что для анализа приспособляемости пористых геоматериалов необходимо учитывать дополнительное поле напряжений. В этом подразделе воздействие на материалы из-за чередующихся условий смачивания и высыхания рассматривается как переменное давление воды, приложенное к внутренней границе () модели полой сферы.
Аналогично построению поля напряжений (20) при чисто гидростатической нагрузке также предлагается дополнительное микроскопическое поле напряжений в следующем виде: в котором фиктивный упругий отклик и соответствующее поле остаточных напряжений при переменном давлении воды равны где максимальное значение давления воды и дополнительная константа. В технике давление воды обычно колеблется в пределах .
Следовательно, исходя из уравнений (19) и (40), общее напряжение на микроуровне, включая влияние давления воды, составляет
После вывода критерия приспособляемости (из уравнения (26) в уравнение (38)) в предыдущем подразделе можно получить новый макроскопический критерий для прогнозирования долговременной стабильности пористых геоматериалов с учетом чередующихся условий смачивания и высыхания:
в котором это условие приспособляемости должно быть выполнено во избежание разрушения из-за переменных нагрузок во всей модели.
Соответствующие выражения и даются уравнением (39).
Сравнивая с макроскопическим критерием в предыдущем подразделе, из предложенного (43) можно сделать вывод, что наличие переменного давления воды уменьшит эффективное среднее напряжение и, наконец, снизит несущую способность рассматриваемого материала. Амплитуда изменения внутреннего давления воды в основном зависит от уровня воды в геоматериалах. Подробные сравнения будут полностью обсуждены в следующем разделе.
4. Численная проверка с помощью пошаговых вычислений МКЭ
Этот раздел посвящен проверке точности предложенного макроскопического критерия пористых геоматериалов путем сравнения с численными результатами. Упругопластическое численное моделирование выполняется программным обеспечением Abaqus поэтапно для анализа переходной фазы перед приспособляемостью или обрушением.
4.1. Реализация расчета на основе FEM
Из-за геометрической симметрии рассматривается только четверть модели полой сферы, дискретизированной 1500 осесимметричными элементами (см.
рис. 6), которая достаточно уточнена для получения надежных результатов.На внешней границе ставится однородное краевое условие.
Как показано на Рисунке 4, только 3 пути критической циклической нагрузки, содержащие все вершины, необходимо учитывать для расчета предельной нагрузки при приспособляемости, если не учитывать изменение внутреннего давления воды. Напротив, при чередующихся условиях смачивания и высыхания область нагрузки изменяется, как показано на рисунке 7, расположенной в первом и втором квадрантах. Следовательно, для выполнения условия приспособляемости необходимо учитывать 4 пути критической циклической нагрузки.
Тем не менее, трехосность макроскопического напряжения определяется вершиной, описывающей форму прямоугольной области нагрузки. Кроме того, трехосность напряжений для всей циклической траектории нагрузки остается постоянной в одном цикле, что реализуется в Abaqus с помощью многоточечной подпрограммы ограничения (MPC), удовлетворяющей заданному граничному условию однородного поля скоростей.
Заметим, что такая подпрограмма ПДК впервые представлена при исследовании полимерных материалов [38], а затем применена в ряде пластичных пористых сред [30, 32, 35] с тем же граничным условием.
Вышеупомянутая процедура расчета выполняется для приложенного значения трехосности напряжения со 100 циклами. Долговременная стабильность рассматриваемого материала оценивается на переходном этапе перед приспособляемостью или обрушением. На практике накопленная эквивалентная пластическая деформация в «опасной» точке будет проверяться в переходной фазе, которая предполагается постоянной, если она находится в приспособляемом состоянии. Увеличивая приложенную нагрузку, достигается предел приспособляемости, когда происходит разрушение из-за усталости или постепенного разрушения.
Циклические отклики на внутренней границе на экваторе полой сферы в состоянии приспособляемости с представлены на рис. 8. Рассмотрены пористость и , твердой фазы. Можно заметить, что после переходной фазы пластическая реакция постепенно прекращается.
Кривая деформация-напряжение имеет тенденцию совпадать в каждом цикле, что соответствует трем критическим путям нагрузки, как показано на рисунке 4.
Описанные пошаговые расчеты выполняются со следующими параметрами в таблице 1.Кроме того, также рассматриваются различные случаи угла трения и 20° с максимальным давлением воды и 0,28 МПа.
4.2. Сравнение и проверка предложенного макроскопического критерия. °. Параметры материала и приняты. Из-за осевой симметрии области приспособляемости (см. рис. 5) и существования отрицательных напряжений в инженерно-геологических работах будет сравниваться и обсуждаться только часть в четвертом квадранте. В целом (рис. 9–11) можно наблюдать соответствие между результатами, полученными по предложенному макроскопическому критерию, и пошаговыми расчетами, свидетельствующее о том, что установленный критерий обладает способностью предсказывать долговременная сохранность рассматриваемых пористых геоматериалов при переменных гидромеханических нагрузках. Более того, для случая чистой гидростатической нагрузки () аналитическое решение (см. вывод в [34]) соответствует значению численного из-за того, что построенное поле микроскопических напряжений является точным.С другой стороны, при увеличении сдвигающих нагрузок () отмечаются небольшие различия из-за аппроксимации девиаторной части поля пробных напряжений. Приложенные поля упругих и остаточных напряжений в среднем удовлетворяют статически допустимому условию, которое может быть улучшено более точным решением. Благодаря статической теореме приспособляемости предлагаемый критерий дает квазинижнюю оценку. С учетом 1 единственного рисунка (рисунки 9 или 10) область эффективных безопасных нагрузок ограничена сплошными линиями, в которых синие и красные линии представляют поверхности текучести предложенного критерия с давлением воды и , а зеленая линия предельная поверхность предельного анализа [29].Можно сделать вывод, что длительная прочность геоматериалов явно снижается из-за изменения давления воды. Уменьшение «ширины» поверхности текучести можно оценить отношением . Кроме того, вокруг области чисто девиаторной нагрузки () эффективная область безопасности определяется предельным критерием, основанным на анализе (10). Разрушение материала происходит за счет развития механизма (постепенное разрушение в первом цикле нагружения) вместо усталости. На рис. 11 показано сравнение аналитических и численных результатов при давлении воды МПа.Максимальное значение давления воды является постоянной величиной, которая отличается от двух предыдущих случаев, показанных на рисунках 9 и 10. 5. ЗаключениеВ этой статье был установлен макроскопический критерий, основанный на статической теореме приспособляемости, для прогнозирования долговременной прочности пористых геоматериалов в условиях попеременного увлажнения и высыхания. В рамках микромеханики пористых материалов принята модель полой сферы Гурсона, а эффекты попеременного смачивания и высыхания рассматриваются как переменное внутреннее давление.Полученный критерий зависит от первого и второго инвариантов макроскопического тензора напряжений, коэффициента Пуассона и пористости. Наблюдается снижение эффективной области безопасности из-за попеременного режима смачивания в зависимости от амплитуды изменения давления воды. В конце была оценена точность аналитического решения путем сравнения с результатами пошаговых расчетов на основе МКЭ. В перспективе необходимы особые усилия по повышению точности аналитического решения при девиаторных нагрузках. Доступность данныхДанные, использованные для подтверждения результатов этого исследования, можно получить у соответствующего автора по запросу. Конфликт интересовАвторы заявляют, что у них нет финансового или нефинансового конфликта интересов. Благодарности Авторы благодарят Национальный фонд естественных наук Китая (грант No.11 1708 Конституционное моделирование геоматериалов: разработка, внедрение и оценка эффективностиМаджид Т. Манзари , Университет Джорджа Вашингтона Ричард А. Регейро , Университет Колорадо, Боулдер Вайчинг (Стив) Сан, Колумбийский университет Мотыга И. Анализ многих систем гражданской инфраструктуры включает точное моделирование геоматериалов. В частности, сложный характер связных и несвязных грунтов в сухих, частично насыщенных и насыщенных условиях создает серьезные проблемы моделирования, когда материал подвергается различным путям напряжения / деформации, которые вызванные монотонной и циклической нагрузкой. Более того, зависимость от давления, чувствительность к скорости, изменения текстуры/ткани из-за механических, биотермических, химических процессов, заметное снижение средних эффективных напряжений в водонасыщенных грунтах, подвергающихся циклическим нагрузкам, являются ключевыми характеристиками, которые необходимо учитывать во многих приложениях геомеханики.Недавние достижения в конститутивном моделировании геоматериалов предоставили многообещающие платформы для решения многих из этих сложных явлений. В дополнение к проблемам, связанным с формулировкой подходящей конститутивной модели для геоматериалов, эффективная реализация недавно разработанных моделей, охватывающих широкий диапазон деформаций, создает дополнительный набор проблем, которые редко встречаются в других материалах. Целью этого мини-симпозиума является объединение исследователей, разрабатывающих новые конститутивные модели геоматериалов, внедряющих существующие или новые модели материалов для крупномасштабного моделирования задач геомеханики или оценивающих эффективность существующих или вновь разработанных моделей при различных граничных значениях. проблемы, варьирующиеся от квазистатических до динамических условий нагружения. Особенно приветствуются вклады в усовершенствованные модели упругопластичности, вязкопластичности и пластичности при повреждении, сформулированные в рамках стандартной или расширенной (градиентной, микроморфной и т. д.) структуры континуума для насыщенных и частично насыщенных геоматериалов, а также моделей на основе микромеханики и нейронных сетей. Вычислительная геомеханика | USNCCM 16Цюши Чен, Университет Клемсона WaiChing Sun, Колумбийский университет Хосе Андраде, Калифорнийский технологический институт Рональд Борха, Стэнфордский университет РИчард Регейро, Университет Колорадо Шабнам Семнани, Калифорнийский университет, Сан-Диего Сон Хонг На, Университет Макмастера Геоматериалы, такие как почва, горная порода и бетон, представляют собой многофазные пористые материалы, макроскопические механические свойства которых определяются гранулометрическим составом и формой зерен, минералогическим составом, флюидонасыщением, условиями дренирования, путями и скоростями нагружения, поровым пространством, температурой, химическим составом.
Этот мини-симпозиум станет площадкой для презентаций и дискуссий о последних достижениях в области вычислительной геомеханики. Акцент будет сделан на новых формулировках, вычислительных методах и численном моделировании, связанных с проблемами геоматериалов и геомеханики.Вклады запрашиваются, но не ограничиваются: (1) разработка, внедрение и проверка передовых конститутивных моделей; (2) дискретная и континуальная постановки задач геомеханики; (3) вычислительные модели и алгоритмы для мультифизических задач; (4) многомасштабное моделирование; (5) бессеточные методы для задач больших деформаций; 6) численное моделирование процессов разрушения, повреждения и фрагментации геоматериалов; (7) нелокальное и/или обобщенное континуальное моделирование; 8 – динамика геоматериалов; (9) основанные на данных подходы к задачам геомеханики. границ | От редакции: Гидромеханическое сцепление и поведение геоматериалов при ползучести Тема нашего исследования Frontiers сначала была сосредоточена на гидромеханическом (ГМ) поведении геоматериалов. Гидромеханическое (ГМ) соединение геоматериалов, относящееся к взаимодействию между жидкостью и твердым телом на месте напряженной среды, является существенным фактором воздействия на стабильность инженерно-геологических работ. Terzaghi (1943) впервые предложил принцип эффективного напряжения и установил одномерную модель консолидации однородных насыщенных геоматериалов, которая является базовой теорией и исходной моделью гидромеханического сцепления геоматериалов, а затем Boit (1954, 1956) заложил теоретическое обоснование гидромеханического сцепления путем распространения теории Терцаги на изучение трехмерной консолидации.Уизерспун и др. (1980) впервые определили термин «эффект связи» и выдвинули соответствующую теорию связи. С тех пор исследования поведения гидромеханического сцепления всегда были предметом пристального внимания из-за очень нелинейного и сложного процесса сцепления. На сегодняшний день появилось множество моделей гидротермальной связи для изучения эффекта взаимодействия фильтрации и напряжения в массивах горных пород на основе либо модели дискретной среды (Indraratna 1995; Wang 2000; Zhang 2015; Ren et al., 2017), либо модели сплошной среды модель (Suresh, 2014; Shojaei, et al., 2014; Чжан, 2017). Некоторое соответствующее численное моделирование включает метод конечных элементов (FEM), расширенный метод конечных элементов (XFEM) и метод дискретных элементов (DEM). Вышеуказанные методы раскрывают механизм просачивания в трещинах горных пород. Тем не менее, есть некоторые существенные недостатки. Исследование фильтрационной непроницаемости геоматериалов при гидромеханическом соединении во многом зависит от лабораторного эксперимента. Предварительно установлены взаимосвязи между такими параметрами, как поврежденность, объемное расширение, пористость и проницаемость.Однако для инженерного массива горных пород наличие и развитие сети трещин в горных породах усложняет приведенные выше зависимости. Развитие сети трещин в горных породах, приводящее к изменению связности трещин, обогащает путь потока воды и напрямую приводит к изменению поля фильтрации; в то же время изменение поля фильтрации, влияющее на поле напряжений, вызывает изменение сети трещин. Фильтрационное разрушение инженерного массива горных пород при некоторых сложных стрессовых условиях (напр. Ползучесть различных геоматериалов в качестве еще одного направления исследований было изучено в нашей исследовательской теме Frontiers. Характеристики ползучести геоматериалов очень важны для оценки долгосрочной стабильности инженерно-геологических работ. Ползучесть геоматериалов приводит к деформации, зависящей от времени, и разрушению инженерно-геологических работ.Григгс (1939) впервые провел испытания на ползучесть песчаника, сланца и алевролита и предложил логарифмическую эмпирическую формулу, отражающую определяющую зависимость ползучести горных пород, а затем Лангер (1979) систематически изложил основные понятия и законы ползучести геоматериалов при четвертая Международная конференция по механике горных пород. С тех пор исследования ползучести геоматериалов всегда привлекали большое внимание. На сегодняшний день предложено множество методов испытаний на ползучесть, таких как одноуровневое нагружение, многоуровневое нагружение и многоуровневые циклы нагружения и разгрузки, среди которых многоуровневое нагружение является распространенным и удобным оперативным методом. Лабораторные испытания геоматериалов на ползучесть обычно проводят многоуровневым нагружением от низких до высоких напряжений, а результаты испытаний на ползучесть упорядочивают по принципу линейной суперпозиции для получения непрерывных кривых ползучести. Однако характеристики ползучести мягких пород обычно сильно нелинейны при высоком уровне напряжения, что может не соответствовать принципу линейной суперпозиции.Таким образом, новые экспериментальные методы для точного захвата кривых ползучести при различных уровнях напряжения должны быть изучены дополнительно. Для исследований определяющих моделей ползучести предложенные определяющие модели ползучести обычно рассматривали параметры модели как постоянные, что представляет собой так называемые проблемы линейной ползучести. Прежде всего, гидромеханическое сцепление и поведение геоматериалов при ползучести демонстрируют временную зависимость и высокую нелинейность.Мы надеемся, что этот сборник статей по теме исследования может еще больше обогатить область исследований. Вклад авторов Все перечисленные авторы внесли существенный, непосредственный и интеллектуальный вклад в работу и одобрили ее для публикации. ФинансированиеЭто исследование поддерживается Национальным фондом естественных наук Китая (№№ 51774131, 51774107, 51774322). Конфликт интересовАвторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов. БлагодарностиМы хотели бы поблагодарить всех рецензентов и всех авторов. Мы также хотели бы поблагодарить команду Frontiers за их поддержку и предложения. СсылкиБойт, Массачусетс (1956). Общее решение уравнения упругости и уплотнения для пористого материала. Дж. Заявл. мех. 23 (1), 91–96. Google Scholar Бойт, Массачусетс (1954). Теория упругости и консолидации пористого анизотропного грунта. Дж.заявл. физ. 26, 182–191. doi:10.1063/1.1721956 Полный текст CrossRef | Google Scholar Индраратна, Б. (1995). «Гидромеханические аспекты трещиноватой горной среды», в трудах 8-го конгресса ISRM, международного общества горной механики, Токио, Япония, 25–29 сентября 1995 г. Google Scholar Лангер, М. (1979). «Реологическое поведение горных масс», в материалах 4-го Конгресса Международного общества механики горных пород, Монтрё, Швейцария, 2–8 сентября 1979 г., 3, стр. 29–стр. 62. Google Scholar Рен Ф., Ма Г. В., Фан Л. Ф., Ван Ю. и Чжу Х. Х. (2017). Эквивалентные дискретные сети трещин для моделирования потока жидкости в сильно трещиноватом массиве горных пород. англ. геол. 229, 21–30. doi:10.1016/j.enggeo.2017.09.013 Полный текст CrossRef | Google Scholar Shojaei, A., Taleghani, A.D., and Li, G. (2014). Континуальная модель разрушения при гидроразрыве пористых пород. Междунар. Дж. Пласт. 59 (8), 199–212.doi:10.1016/j.ijplas.2014.03.003 CrossRef Полный текст | Google Scholar Сингх, К.К., Сингх, Д.Н., и Ранджит, П.Г. (2015). Лабораторное моделирование течения через одиночный трещиноватый гранит. Каменный мех. Рок инж. 48 (3), 987–1000. doi:10.1007/s00603-014-0630-9 Полный текст CrossRef | Google Scholar Суреш, К. CrossRef Полный текст | Google Scholar Wang, HT (2000). Анализ устойчивости водонасыщенного скального откоса с просачиванием сетей трещин и сопряжением дискретных элементов. Гидрогеол. англ. геол. 27 (2), 30–33. Google Scholar Уизерспун П.А., Ван Дж. и Иваи К. (1980). Справедливость кубического закона для течения жидкости в деформируемой трещине горной породы. Водный ресурс.Рез. 16 (6), 1016–1024. doi:10.1029/WR016i006p01016 Полный текст CrossRef | Google Scholar Zhang, GX (2017). Исследование метода численного моделирования, используемого при анализе влияния фильтрационного давления в сплошной среде с порами на деформации и напряжения. Дж. Гидравл. англ. 48 (6), 640–650. Полный текст CrossRef | Google Scholar Zhang, QH (2015). Генерация методом конечных элементов произвольных трехмерных сетей трещин для анализа потока в сложных дискретных сетях трещин. Дж. Гидрол. 529, 890–908. doi:10.1016/j.jhydrol.2015.08.065 Полный текст CrossRef | Google Scholar Чжао Ю., Чжан Л., Ван В., Тан Дж., Линь Х. и Ван В. (2017b). Нестационарный импульсный тест и морфологический анализ одиночных трещин горных пород Int. J Rock Mech Мин. 91, 139–154. doi:10.1016/j.ijrmms.2016.11.016 CrossRef Полный текст | Google Scholar Чжао Ю., Чжан Л., Ван В., Ван В. и Ма В. (2018). Разделение упруговязкопластических деформаций породы и нелинейная модель ползучести. Междунар. Дж. Гео Мех. 18 (1), 04017129. doi:10.1061/(ASCE)GM.1943-5622.0000163, 697–710 CrossRef Полный текст | Google Scholar Чжао Ю. Л., Ван Ю. X., Ван У. Дж., Ван В. и Тан Дж. З. (2017a). CrossRef Full Text | Google Scholar Чжао Ю. Л., Чжан Л. Ю., Ван В.J., Wan, W., Li, S.Q., Ma, W.H., et al. (2017с). Ползучесть неповрежденного и растрескавшегося известняка при многоуровневых циклах нагружения и разгрузки. Каменный мех. Рок инж. 50 (6), 14. doi:10.1007/s00603-017-1187-1 CrossRef Full Text | Google Scholar Циммерман, Р. В., и Бодварссон, Г. С. (1996). Гидравлическая проводимость трещин горных пород. Пер. Пористая среда 23, 1–30. doi:10.1007/BF00145263 Полный текст перекрестной ссылки | Google Scholar Гипопластическое и послеаварийное моделирование геоматериалов / Геотехническая наука и инженерия / Институты и центры / Научные исследования / Университет Ньюкасла, АвстралияНовая гипопластическая модель для глины Конститутивные модели играют ключевую роль в прогнозировании поведения
геотехнические проблемы, которые часто очень сложны. Точная формулировка этой тензорной функции требует надежного
понимание поведения почвы. Простой гипопластический конститутивный
уравнение было разработано в Ньюкасле, которое может зафиксировать,
количественно реакция нормально сцементированной глины при осушенном
и недренированные тесты.
Численное моделирование поведения после отказов гранулированных материалов Гранулированные материалы широко встречаются в гражданском строительстве и
другие инженерные дисциплины.Типичные примеры включают песок, гравий,
щебень, соль, сахар, крупы и фармацевтические препараты. В таком
материалы, напряжения передаются при прямом контакте между зернами
и, из-за их дискретного характера, общее поведение очень
сложный.
| |||||||||||||||||||||||||||||||
Соответствующая поверхность текучести была перемещена вправо, и область безопасности соответственно уменьшилась.
Применение этого метода для структурных расчетов также является сложной темой.
Линг , Колумбийский университет 
Следовательно, многие из методов реализации, которые изначально были разработаны для других инженерных материалов, сталкиваются со значительными проблемами при применении к конститутивным моделям для геоматериалов.
реакции и другие факторы.В результате прогнозирование механического поведения геоматериалов часто требует знаний о том, как несколько процессов, которые часто происходят в разных пространственных и временных областях, взаимодействуют друг с другом в различных масштабах.
Для почвы и неповрежденной породы, которые считаются пористой средой, во время процесса просачивания давление поровой жидкости как внешнее напряжение, приложенное к матрице пористой среды, изменит эффективное напряжение пористой среды, которое отражает действие поровой жидкости на напряжение.И наоборот, изменение эффективного напряжения приведет к изменению проницаемости и пористости пористых сред, что отражает влияние напряжения на просачивание. Для массивов трещиноватых горных пород поток воды в трещинах вызовет изменение раскрытия трещины (Zimmerman and Bodvarsson, 1996; Singh, et al., 2015; Zhao, et al., 2017b). И наоборот, изменение апертуры трещин будет влиять на коэффициент проницаемости и фильтрацию трещин в горных породах. Таким образом, коэффициент проницаемости как связующее звено между полем напряжений и полем фильтрации является динамической переменной при анализе гидромеханической связи.Некоторые ранее предложенные модели гидромеханической связи, которые предполагали, что коэффициент проницаемости остается постоянным, могут отражать только влияние фильтрации на поля напряжений, но не могут отражать влияние напряжений на поля фильтрации.
Таким образом, все еще необходимы дальнейшие исследования поведения гидромеханического сцепления геоматериалов, такие как фильтрационные характеристики пористых и трещинных сред, новые экспериментальные и численные методы в области гидромеханического сцепления. Чтобы раскрыть законы гидромеханического сцепления геоматериалов, Our Frontiers Research Topic опубликовал несколько инновационных статей, связанных с гидромеханическим сцеплением.Для экспериментальных исследований Deng et al. проведены инфильтрационные суффозионные испытания, которые показали, что появление неравномерных локальных гидравлических градиентов вдоль пути течения в почве является признаком начала суффозии. Йо и др. использовал газообразный гелий под высоким давлением для измерения проницаемости песчаника и предложил метод поверхности отклика для изучения влияния всестороннего давления, внутреннего давления, эффективного напряжения и давления воды на газопроницаемость, обеспечивая техническую поддержку для улучшения проницаемости песчаника.
Чжэн и др. изучено влияние влажности угля на прочность, модель распространения трещин и пористую структуру. Они обнаружили, что микропоры и мезопоры в угле превращаются в более крупные поры, в то время как режим разрушения меняется с разрушения при растяжении на разрушение при растяжении-сдвиге с увеличением содержания влаги в угле. Приведенные выше экспериментальные исследования показали, что наличие жидкости в порах и трещинах может привести к изменению микроструктуры геоматериалов, а фильтрационное давление влияет на распределение поля напряжений в геоматериалах.Моделирование течения жидкости в различных средах было в центре внимания текущей темы. Ли и др. разработала модель сопряжения Дарси-Навье-Стокса для изучения потока грунтовых вод и их передачи в карстовом водоносном горизонте. Се и др. предложил конститутивную модель статистического повреждения при сдвиге соединений горных пород, содержащих фильтрационное давление, и определил параметры модели, связанные с фильтрационным давлением.
Кроме того, в данной теме также было исследовано влияние гидротермальной связи на механическое и деформационное поведение породы при разрушении.Чжао и др. исследовали влияние гидротермической обработки на механическое поведение песчаника и обнаружили, что высокая температура, высокое давление воды и методы охлаждения могут влиять на механические параметры песчаника.
С одной стороны, хотя модели дискретной среды могут эффективно описывать неоднородные и анизотропные гидравлические свойства трещин, модели не в состоянии определить геометрические параметры всех трещин в горных массивах.С другой стороны, модели сплошной среды рассматривают систему сети трещин горных пород как эквивалентную сплошную среду некоторыми эквивалентными методами, которые просты и обладают сильной способностью к адаптации. Однако эти непрерывные модели не могут описать поведение крупных трещин в массивах с высокой проводимостью. Помимо объяснения эффекта просачивания, другой задачей является учет эволюции повреждений, которая заключается в следующих двух аспектах: 1) течение флюидов в массивах пород приводит к изменению порового давления и деформации горных пород и повреждению массивов горных пород; 2) повреждение увеличивает проницаемость горных массивов, что является ключевым параметром, связанным с фильтрационной характеристикой, и ухудшает жесткость горных массивов, которая является ключевым параметром, связанным с механическими характеристиками.
По-видимому, два вышеупомянутых нелинейных процесса связаны с эффектом гидродинамической связи и развитием повреждений, и оба могут быть объединены в связь просачивания и разрушения. Однако мало внимания уделялось этому сложному взаимодействию просачивания и разрушения.
г. нарушение строительства, влияние замкнутого водоносного горизонта и т. д.) все еще находятся на стадии разведки. Предстоит большая работа по изучению закономерностей фильтрационного разрушения инженерного массива горных пород при гидромеханической связи.
В настоящее время исследования поведения геоматериалов при ползучести сосредоточены на испытаниях на ползучесть, определяющих моделях ползучести и численном моделировании.Испытания геоматериалов на ползучесть могут выявить механические свойства ползучести геоматериалов при различных уровнях нагрузки и предоставить соответствующие параметры ползучести для создания соответствующих моделей критического и численного анализа ползучести. Конститутивные модели ползучести могут быть предложены путем соединения вязких, упругих и пластичных элементов параллельно или последовательно. Для конкретной инженерной геологии выбор одной или двух подходящих моделей ползучести, а затем определение соответствующих параметров ползучести, является актуальной проблемой, требующей решения в инженерии.Что касается ползучести почвы, Chen et al. провел испытания кораллового песка на ползучесть, выявив закономерности эволюции фракталов и дробления частиц в процессе ползучести. Он и др. и Сюэ и др. изучали характеристики ползучести крупнозернистого грунта и красной глины в условиях трехосного сжатия соответственно.
Для характеристики ползучести горных пород Чжао предложил новый экспериментальный метод для отделения компонентов вязкоупругой и вязкопластической деформации от общей деформации ползучести и установил некоторые модели упруговязкопластической ползучести для реализации разделения деформации (Чжао и др., 2017а; Чжао и др., 2017c; Чжао и др., 2018). Лю и др. исследовал характеристики разрушения мрамора при ползучести при высоких нагрузках с использованием метода акустической эмиссии (АЭ), который предлагает новую идею для прогнозирования разрушения породы при ползучести. Чтобы изучить характеристики ползучести при сдвиге анкерной конструкции, Wang et al. предложил нелинейную модель ползучести для анализа поведения вязкопластической деформации анкерной конструкции. Чтобы изучить влияние слабой прослойки на поведение ползучести породы, Тан и Чжао изучили влияние слабого угла наклона прослойки на свойства ползучести песка и наблюдали, как мгновенная упругая и мгновенная пластическая деформации увеличиваются с увеличением слабого угла наклона прослойки.
Однако многие эксперименты с ползучестью породы показали, что механические параметры (например, модуль упругости, прочность и вязкость) зависят от времени. Таким образом, параметры ползучести следует рассматривать как нестационарные переменные, отражающие нелинейные вязкие характеристики породы.Как установить некоторые нелинейные модели ползучести с нестационарными переменными, заслуживает дальнейшего изучения. Влияние размера на поведение ползучести также является важным исследовательским вопросом. Отмечено, что параметры ползучести лабораторных образцов по-прежнему не могут точно отражать характеристики ползучести инженерной горной массы из-за более сложных геологических структур инженерной горной массы.
Г. (2014). Математическое моделирование потока подземных вод и переноса растворенных веществ в насыщенных трещинами породах с использованием подхода двойной пористости. Дж. Гидрол. англ. 19 (12), 04014033. doi:10.1061/(ASCE)HE.1943-5584.0000986
doi:10.13243/j.cnki.slxb.20161087
Моделирование нелинейного реологического поведения твердых пород с помощью трехосного реологического эксперимента. Междунар. Дж. Рок Мех. Мин. 93, 66–75. doi:10.1016/j.ijrmms.2017.01.004
Общепринятый
упругопластические модели, хотя и широко используемые и очень мощные, имеют
трудность описания изменения тангенциальной жесткости в зависимости от
направление приращения деформации и дилатансия сдвига в режиме упрочнения.
Было предложено много новых типов конститутивных моделей для преодоления
эта проблема, такая как модели ограничивающих поверхностей, модели подзагрузки и
гипопластические модели. Среди этих общих подходов к пластичности
гипопластические модели обладают достоинствами ясной физической концепции, простого
математическая формулировка и простая численная реализация.В
гипопластичности, приращение напряжения-деформации описывается
нелинейная тензорнозначная функция.
Модель требует всего 5 ключевых параметров, которые могут
легко определить с помощью лабораторных исследований.На рисунках ниже показаны
предсказания предложенной нами модели для глины Фудзиномори под осушенным и
недренированные испытания на сдвиг.
Гранулированный материал течет несколько иначе, чем обычный
жидкость, так как она может выдерживать напряжение сдвига, как твердое тело, когда оно ограничено. То
прочность на сдвиг в основном определяется интерактивным трением между
зерна, форма, размер и твердость которых играют существенную роль.То
макрореакция гранулированного материала также сильно зависит от
пустот (или плотности набивки) и приложенным ограничивающим давлением
к этому.
шаблон для опоры на песке.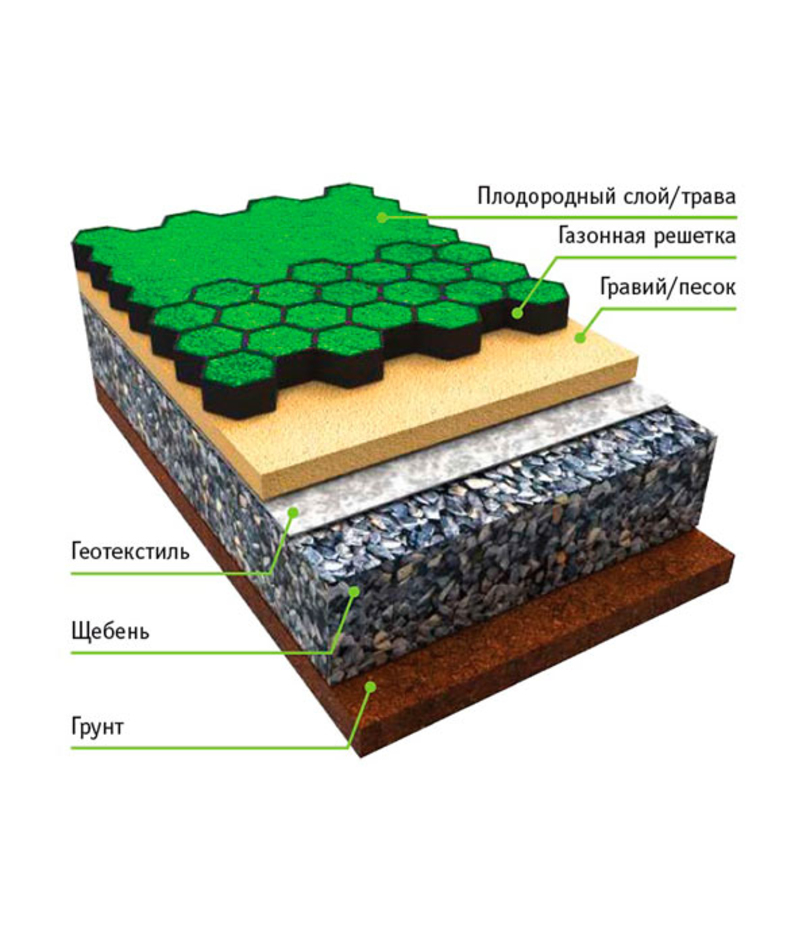
науч. 10 (1), 1–8 (2020).
Энергетика 181 , 1285 (2019).
, Чо, Х. и Део, М. Экспериментальное и молекулярное моделирование точек кипения смесей углеводородов в нанопористых средах. Энергетическое топливо 31 , 3427 (2017).
Дж. Импакт Инж. 120 , 138 (2018).
и Агар С. Использование 3D-печати на основе смолы для создания геометрически точных прототипов пористых осадочных пород. Подземные воды 56 (3), 482 (2018).
, Yoon, H., Bobet, A. & Pyrak-Nolte, L.J. Минеральная ткань как скрытая переменная в образовании трещин в слоистых средах. науч. 10 , 1–9 (2020).
).
).
Laser Photonics Rev. 7 , 22 (2013).
).
Проведя три года в Норвегии, я почувствовал необходимость вернуться в Тампере, место, где я провел лучшее время в своей жизни и которое считаю своим вторым домом.В настоящее время я работаю специалистом по геотехнике в компании Ramboll и по совместительству научным сотрудником PostDoc в Университете Тампере, где я изучаю сложные геоматериалы.
В то же время возможности отдела уникальны, и вы получаете всю поддержку и инструменты, необходимые для достижения ваших целей.Итак, в целом замечательный опыт.
Там вы не только делитесь и учитесь, но и знакомитесь с несколькими людьми и заводите новых друзей. Кроме того, я могу сказать, что мой период обмена, проведенный в Национальном университете Сингапура (NUS), был одним из самых ярких моментов моего обучения в докторантуре. Международное сотрудничество является ключом к успеху в исследованиях, и период обмена открыл двери для установления плодотворного сотрудничества между Университетом Тампере и NUS и дал мне незабываемый жизненный опыт.