Площадь четырехугольника
Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн.
Площадь четырехугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.
Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.
В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.
1
Площадь четырехугольника по диагоналям и углу между ними
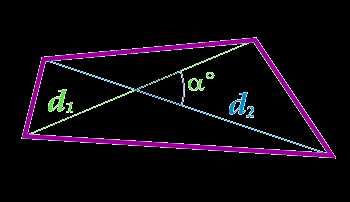
d1 — диагональ
α° — угол между диагоналями
… подготовка …
2
Площадь четырехугольника через стороны и углы между этими сторонами
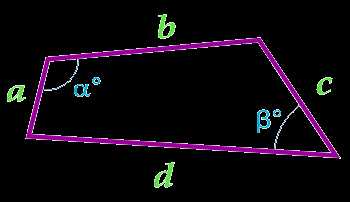
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
a — сторона
b — сторона
c — сторона
d — сторона
α° — угол между сторонами
β° — угол между сторонами
… подготовка …
3
Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты
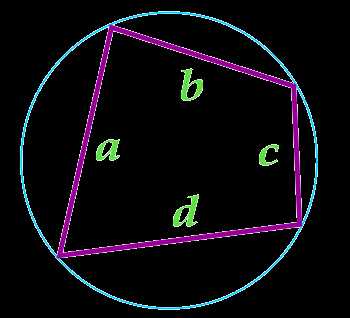
Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
a — сторона
b — сторона
c — сторона
d — сторона
… подготовка …
4
Площадь четырехугольника в который можно вписать окружность
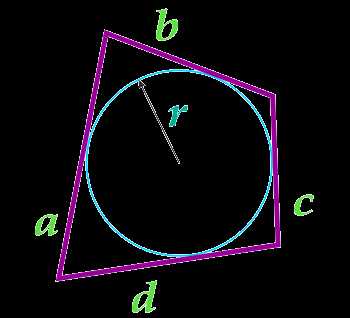
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
a — сторона
b — сторона
c — сторона
d — сторона
r — радиус вписанной окружности
… подготовка …
5
Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними
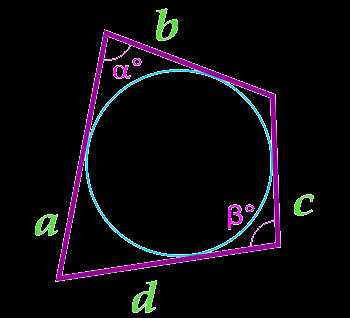
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
a — сторона
b — сторона
c — сторона
d — сторона
α° — угол между сторонами
β° — угол между сторонами
… подготовка …
Определения
Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться нашим «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
doza.pro
Формулы вычисления площади произвольного четырёхугольника — Сделай дом
Четырехугольником называется фигура, состоящая из четырех вершин, три из которых не лежат на одной прямой, и отрезков, соединяющих их.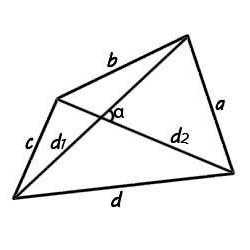
Существует множество четырехугольников. К ним относятся параллелограммы, квадраты, ромбы, трапеции. Найти площадь квадрата можно найти по сторонам, площадь ромба легко вычисляется по диагоналям. В произвольном четырехугольнике также можно использовать все элементы для вывода формулы площади четырехугольника. Для начала рассмотрим формулу площади четырехугольника через диагональ. Для того, чтобы ее использовать потребуются длины диагоналей и размер острого угла между ними. Зная необходимые данные можно проводить пример расчета площади четырехугольника по такой формуле:
Половина произведения диагоналей и синуса острого угла между ними является площадью четырехугольника. Рассмотрим пример расчета площади четырехугольника через диагональ.
На примере расчета площади четырехугольника через диагонали понимаем, что формула очень похожа на расчет площади параллелограмма.
Площадь четырехугольника по сторонам
Когда известны длины сторон фигуры, можно применить формулу площади четырехугольника по сторонам. Для применения этих расчетов потребуется найти полупериметр фигуры. Мы помним, что периметр – это сумма длин всех сторон. Полупериметр – это половина периметра. В нашем прямоугольнике со сторонами a, b, c, d формула полупериметра будет выглядеть так:
Зная стороны, выводим формулу. Площадь четырехугольника представляет собой корень из произведения разности полупериметра с длиной каждой стороны:
Площадь четырехугольника, заданного координатами
Формула площади четырехугольника по координатам используется для расчета площади фигур, которые располагаются в системе координат. В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY.
Как высчитать площадь участка если стороны разные
Площадь четырехугольника представляет собой корень из произведения разности полупериметра с длиной каждой стороны: Рассмотрим пример расчета площади четырехугольника через стороны. Дан произвольный четырехугольник со сторонами a = 5 см, b = 4 см, с = 3 см, d = 6 см.
Для начала найдем полупериметр: используем найденное значение для расчета площади: Площадь четырехугольника, заданного координатами Формула площади четырехугольника по координатам используется для расчета площади фигур, которые располагаются в системе координат.
В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY.
Дан квадрат ABCD, расположенный в системе координат XY.
Калькулятор расчета площади земельного участка неправильной формы
Такой вариант подсчета площади пола более сложный, так как требует вычисления площади фигур, входящих в состав помещения по отдельности.
Для вычисления общей площади следует разбить пространство на несколько правильных фигур, в виде прямоугольников, трапеций, квадратов и т.д.
Например, если помещение имеет г-образную форму, то достаточно его разделить на два прямоугольника, вычислить площадь каждого из них и суммировать полученные результаты.
Площадь участка сложной формы
Минимальное значение площади обычной жилой комнаты составляет восемь метров квадратных. Площадь общей комнаты или гостиной должна составлять от 13 до 23 метров квадратных.
Спальня должна располагаться в углу дома, и быть не проходным помещением.
Если жилая площадь дома или квартиры составляет от 15 до 55 метров квадратных, то минимальная площадь кухни должны быть 6 метров квадратных.
Площадь неправильного четырехугольника с заданными сторонами
В итоге, покупка краски и определение количества отделочного материала для пола выполнится быстро. Не выполняйте замеры по стене, так как она может быть кривой и приведет к возникновению неточности в процессе определения площади пола.
Особой сложностью отличаются работы по определения площади пола, на котором имеются уступы в виде полукруга или волны. Данная ситуация предполагает измерение каждой из дуг, нахождение радиусов и раздробление площади на несколько геометрических фигур.
С помощью определения площади для каждой из них вычисляется общая формула асимметричного сегмента. Определение площади прямоугольной комнаты и потолка Прямоугольное помещение является наиболее типичным и часто встречающимся вариантом.
Для расчета площади достаточно длину помещения умножить на его ширину.
Как вычислить площадь четырехугольника
ВниманиеДля расчета площади пола в такой комнате требуется также разделить пространство на несколько частей, площадь которых вычисляется по отдельности. Бывают варианты помещений, которые имеют разные уровни пола, то есть возвышенности или уклоны.
Таким образом, помещение разделяется на несколько зон.
Например, в кухне выделяется столовая и рабочая части. То же самой и бывает с потолком, например, многоуровневым.
Для вычисления площади пола с уступами или возвышенностями, следует опять же разделить пространство на части в виде прямоугольников или квадратов, а те самые выступы, измерить линейкой и вычислить их площадь.
Таким способом получится провести расчет общей площади помещения.
Учтите, что в таком случае предпочтительно использовать рулетку, которая устанавливается вблизи основания. Кроме того, потребуется карандаш и тетрадь, для записывания всех значений.
Площадь земельного участка
ВажноПри планировке кухни в зданиях с жилой площадью более 55 квадратных метров, кухня должна занимать минимум пятую часть всего дома.
Если кухня занимает более 10 квадратных метров, возможен вариант ее использования в качестве столовой или комнаты для приема гостей. Минимальная ширина прихожей составляет 140 см, в ней также должно присутствовать естественное освещение.
Для детской комнаты достаточно площади в 10-15 метров квадратных. Самыми маленькими должны быть ванная и туалет. Их площадь ровняется 4-8 квадратным метрам.
Площадь четырехугольника
С помощью линейки и угольника разделите пространство на несколько зон, в виде правильных фигур. 4. Каждую из сторон фигуры следует измерить и обозначить в проекте. 5.
Согласно формуле для расчета площади фигуры определите значения каждой из них и суммируйте полученные результаты.
Как определить площадь комнаты с неровными стенами При наличии помещения, в котором стены имеют вид многогранников или непрямых непропорциональных фигур, расчеты проводить гораздо сложнее.
Измерить периметр в таком помещении достаточно просто. Следует использовать рулетку и пройти с ней по всей комнате, измеряя каждый из участков по отдельности.
Источник: http://www.kredlikvid.ru/?p=2078
Рассчитать площадь неправильного многоугольника онлайн — Юридические услуги
Правильный пятиугольник – это многоугольник с пятью равными сторонами. Все соседние стороны образуют угол 108°. Формулы
- P – периметр
- S – площадь
- R – радиус K
- r – радиус k
- S’ – центр
- a – сторона
- K – окружность описанная
- k – окружность вписанная
При предоставлении услуг веб-сайт «Calculat.org» использует файлы куки.
Более информации Вы не любите рекламу? Мы ее тоже не любим, тем не менее доходы от рекламы предоставляют возможность функционирования нашего веб-сайта и бесплатного обслуживания наших посетителей. Пожалуйста, подумайте, не стоит ли отменить блокировку рекламы на этом веб-сайте.
Шаг 1: Найдем радиус вписанного круга.А = R * Cos(π / N)= 2 * Cos(3.14 / 5)= 2 * Cos(0.63)= 2 * 0.81Апофема (радиус вписанного круга) = 1.62.Шаг 2: Найдем площадь.Площадь = A² * N * Tan(π / N)= 1.62² * 5 * Tan(3.14 / 5)= 2.62 * 5 * Tan(0.63)= 13.1 * 0.73Площадь = 9.5.
Задача 4: Найти площадь многоугольника используя Апофему (радиус вписанного круга), если длина стороны равна 2, а количество сторон 5.Step 1: Найдем Апофему.Апофема = длина стороны / (2 * Tan(π / N))= 2 / (2 * Tan(π / 4))= 2 / (2 * Tan(0.785))= 2 / (2 * 0.999)= 2 / 1.
998Апофема (А) = 1.
Внимание
Шаг 2: Найдем периметр.Периметр (P) = (N * (длина стороны) = 4 * 2 = 8 Шаг 3: Найдем площадь.Площадь = (A * P) / 2= (1 * 8) / 2= 8 / 2Площадь = 4. Приведенные выше примеры показывают, как вычислить площадь и периметр многоугольника вручную.
Площадь неправильного четырехугольника с заданными сторонами
Расчет площади Многоугольника, используя радиус вписанного круга и длину стороны:[ (A×P)/2 ][ Apothem(A) = side/(2×Tan(π/N)) ] Введите длину = Введите кол-во сторон = Площадь Многоугольника = Расчет площади по длине стороны:Площадь Многоугольника = ((side)² * N) / (4Tan(π / N))Периметр Многоугольника = N * (side) Расчет площади по радиусу описанной окружности :Площадь Многоугольника = ½ * R² * Sin(2π / N) Расчет площади по радиусу вписанного круга :Площадь Многоугольника = A² * N * Tan(π / N)где, A = R * Cos(π / N) По радиусу вписанного круга и длине стороны :Площадь Многоугольника = (A * P) / 2где A = сторона / (2 * Tan(π / N))где,
- N = Количество сторон,
- A = Радиус вписанного круга,
- R = Радиус описанной окрудности,
- P = Периметр
Примеры: Задача 1: Найдите площадь и периметр многоугольника, если длина стороны = 2 и количество сторон = 4.
Площадь четырехугольника
Вычислить Расчет площади правильного многоугольника Многоугольник с числом сторон n и длиной стороны аМногоугольник с числом сторон n, вписанный в окружность радиуса RМногоугольник с числом сторон n, описанный вокруг окружности радиуса r n= 3456789101112131415 a= ммсммкмфутярддюйммиля Вычислить Расчет площади круга Рассчитать площадь круга, если известен: r=ммсммкмфутярддюйммиля Вычислить Расчет площади эллипса a=ммсммкмфутярддюйммиля b=ммсммкмфутярддюйммиля Вычислить Расчет площади сектора круга Рассчитать площадь сектора круга, если известен: r= ммсммкмфутярддюйммиля θ= ммсммкмфутярддюйммиля град.рад.
Шаг 1: Найдем площадь.Площадь = ((длина стороны)² * N) / (4Tan(π / N))= ((2)² * 4) / (4 * Tan(3.14 / 4))= (4 * 4) / 4 * Tan(0.785)= 16 / 4 * 0.999= 16 / 3.996Площадь = 4.
Шаг 2: Найдем периметр.
Периметр = (N * (длина стороны) = 4 * 2 = 8 Задача 2: Найдите площадь и периметр многоугольника, если радиус описанной окружности = 2, количество сторон многоугольника = 5.
Правильный многоугольник
Вычислить Расчет площади трапеции Способ нахождения площади трапеции: По двум основаниям a,b и высоте hПо двум основаниям a,b и боковым сторонам c,d a=ммсммкмфутярддюйммиля b=ммсммкмфутярддюйммиля h= ммсммкмфутярддюйммиля d= ммсммкмфутярддюйммиля Вычислить Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры.
трические единицы измерения площади: Квадратный метр, производная единица системы СИ 1 м2 = 1 са (сантиар) Квадратный километр — 1 км2 = 1 000 000 м2 Гектар — 1 га = 10 000 м2 Ар (сотка) — 1 а = 100 м2 (сотка как правило применяется для измерения земельных участков и равна 100 м2 или 10м х 10м) Квадратный дециметр, 100 дм2 = 1 м2; Квадратный сантиметр, 10 000 см2 = 1 м2; Квадратный миллиметр, 1 000 000 мм2 = 1 м2.
Данный онлайн-калькулятор удобен при расчете площадей помещений и земельных участков.
Калькулятор расчета площади земельного участка неправильной формы
Важно
Полезные калькуляторы Конвертер единиц площади | Конвертер единиц длины Расчет площади прямоугольника a=ммсммкмфутярддюйммиля b=ммсммкмфутярддюйммиля Вычислить Расчет площади треугольника Способ нахождения площади треугольника: По трем сторонамПо одной стороне и высоте, опущенной на эту сторонуПо двум сторонам и углу между ними a=ммсммкмфутярддюйммиля b=ммсммкмфутярддюйммиля c= ммсммкмфутярддюйммиля град.рад. Вычислить Расчет площади параллелограмма Способ нахождения площади параллелограмма:По основанию и высоте параллелограммаПо двум сторонам и углу между нимиПо двум диагоналям и углу между ними a=ммсммкмфутярддюйммиля h=ммсммкмфутярддюйммиля c= ммсммкмфутярддюйммиля град.рад.
Площадь и периметр пятиугольника
- Математические калькуляторы
- Калькулятор для расчета площади
- Данный онлайн-калькулятор позволяет рассчитать площадь различных геометрических фигур, таких как:
- Прямоугольник;
- Параллелограмм;
- Круг;
- Сектор круга;
- Треугольник;
- Правильный многоугольник;
- Эллипс;
- Трапеция.
Для удобства расчетов вы можете выбрать единицу измерения (миллиметр, сантиметр, метр, километр, фут, ярд, дюйм, миля). Также полученный результат можно конвертировать в другую единицу измерения путем выбора её из выпадающего списка.
Площадь участка сложной формы
(Нажмите кнопку «Остановить» для определения площади понравившегося Вам четырехугольника с заданными Вами сторонами).
12345678901234567890 Площадь фигуры: Четырехугольник: Площадь неправильного четырехугольника, зная только длины сторон, вычислить нельзя.
Источник: http://AngelSystem.ru/rasschitat-ploshhad-nepravilnogo-mnogougolnika-onlajn/
Как высчитать площадь участка если стороны разные
С завидным упорством некоторые пользователи Planetcalc оставляют запросы на создание калькулятора для расчета площади неправильного четырехугольника, для которого известны только длины сторон.
Подумалось, что остановить их можно только написав вот такой шуточный калькулятор. (Нажмите кнопку «Остановить» для определения площади понравившегося Вам четырехугольника с заданными Вами сторонами).
12345678901234567890 Площадь фигуры: Четырехугольник: Площадь неправильного четырехугольника, зная только длины сторон, вычислить нельзя.
- для покраски или отделки потолка также следует знать его площадь, практически все лакокрасочные изделия и грунтовки имеют в технических характеристиках показатель расхода на один квадратный метр;
- отделка стен гипсокартоном требует вычисления общей площади стен, для покупки нужного количества материала;
- при найме строителей, например, для отделки пола плиткой, каждый метр квадратный имеет определенную стоимость, которая считается в конце выполнения работ;
- при продаже дома или при его оформлении, такой параметр как жилая площадь, площадь кухни и других комнат также является особо важным.
Площадь комнаты: проведение расчета площади пола Для определения площади пола существуют разные причины: ремонт и покупка материалов для его отделки, проведение теплоизоляции, вычисление полезной площади и т.д.
Площадь участка сложной формы
Например, если длина комнаты составляет 3,40 м, а ее ширина 5,20 м, то для определения площади потолка достаточно 3,40х5,20, в итоге получится 17, 68 метров квадратных площади. Для расчета периметра потолка используется другая формула, которая подразумевает сумму удвоенных его длины и ширины.
Внимание
То есть, периметр потолка ровняется 2х3,40+2х5,20=17,2 м. Поэтому, в процессе закупки профилей, потребуется 17,2 метра материала.
Однако, рекомендуется, даже при проведении точнейших расчетов, покупать материал с запасом в 10-15 процентов, для компенсации различного рода механических повреждений и стыков. Какова площадь комнаты в которой имеются ниши и выступы Для определения площади такого помещения следует изрядно потрудиться и выполнить такие действия: 1.
3.
Площадь неправильного четырехугольника с заданными сторонами
Важно
Полупериметр треугольника рассчитываем так: Р = (А + В + С) / 2 Комната со сложной конфигурацией стен. Фото — welovead.com Особенности расчета площади простых стен и стен, содержащих выступы и ниши Теперь давайте рассмотрим такой важный момент, как расчет площади стен комнаты.
Зная именно эту величину, вы сможете купить нужное количество обоев для ремонта. Конечно, вы можете обратиться к консультанту в строительном магазине, и он обязательно расскажет, как посчитать площадь стен.
В этом нет ничего сложного: измерьте длину, ширину и высоту помещения. Далее площадь стен высчитываем по формуле: Sстен = Р х С, где Р – периметр комнаты, С – высота стен.
Как вычислить площадь четырехугольника
Затевая ремонт, вы должны приобрести достаточное количество обоев, клея, краски и прочих материалов. Для этого вам необходимо знать, как рассчитать площадь комнаты.
Если вы поймете, как получить и применить нужные измерения, то в дальнейшем, например, при покупке или продаже недвижимости, вы сможете самостоятельно посчитать площадь помещения и проверить документы. :
- Простая комната прямоугольной или квадратной формы
- Комната, в которой имеются ниши или выступы
- Комната сложной конфигурации
- Особенности расчета площади простых стен и стен, содержащих выступы и ниши
Простая комната прямоугольной или квадратной формы Для того, чтобы узнать, как рассчитать площадь пола комнаты, вы должны определить его форму. В помещении, которое представляет собой прямоугольник или квадрат, нужно измерить длину и ширину и умножить значения между собой.
Площадь земельного участка
Ровный, прямоугольный потолок без каких-либо ниш и выступов означает, что его необходимо измерить по длине и ширине, а затем посчитать площадь простым умножением. Если вы планируете утеплить пол с помощью нагревательных элементов, то из общей площади пола вам нужно будет вычесть площадь, которая занята тяжелой мебелью.
Комната сложной конфигурации Нередко встречаются комнаты необычной формы. Если есть возможность, то нужно разделить помещение на несколько прямоугольников, посчитать площадь каждого и сложить.
Площадь комнаты в форме круга вычисляется по формуле: S комнаты = πR², где R – радиус. Необходимо учитывать, сколько градусов в секторе.
Для расчета площади комнаты треугольной формы используют формулу Герона: Sкомнаты = √ (P(P -A) х (Р — В) х (Р — С)), где Р – половина периметра треугольника, А, В, С – длины его сторон.
Площадь четырехугольника
Ответы пользователей и экпертов форума на вопрос: Помогите рассчитать площадь земельного участка (4, 5 4, 2 1, 0 1, 4 4, 5 м, ) в чертеже написно 8 соток proc59 0 А в скобках что это за измерения? Как узнать площадь участка Что бы узнать площадь участка необходимо умножить его размеры между… Гость 1 Если все стороны разные по размеру, то берём сумму двух длин делим на два, получается средняя длинаюТакже с шириной. Затем умножаем полученную среднюю длину на ширину и делим на 100. Получиться площадь участка. Гость 0 Здравствуйте! Можно узнать ? Если по документам мне пренадлежат 0. 0131 га — сколько это соток? Гость 0 Здравствуйте! Можно узнать ? Если по документам мне пренадлежат 0.
Источник: http://gc-kzn.ru/kak-vyschitat-ploshhad-uchastka-esli-storony-raznye/
Как высчитать площадь участка если стороны разные | BK
Пусть дан четырехугольник с двумя диагоналями d1=5 см;d2=4см. Острый угол между ними равен α = 30°. Формула площади четырехугольника через диагонали легко применяется для известных условий.
Подставим данные: На примере расчета площади четырехугольника через диагонали понимаем, что формула очень похожа на расчет площади параллелограмма.
Площадь четырехугольника по сторонам Когда известны длины сторон фигуры, можно применить формулу площади четырехугольника по сторонам. Для применения этих расчетов потребуется найти полупериметр фигуры.
Мы помним, что периметр – это сумма длин всех сторон. Полупериметр – это половина периметра. В нашем прямоугольнике со сторонами a, b, c, d формула полупериметра будет выглядеть так: Зная стороны, выводим формулу.
В произвольном четырехугольнике также можно использовать все элементы для вывода формулы площади четырехугольника. Для начала рассмотрим формулу площади четырехугольника через диагональ.
Для того, чтобы ее использовать потребуются длины диагоналей и размер острого угла между ними.
Зная необходимые данные можно проводить пример расчета площади четырехугольника по такой формуле: Половина произведения диагоналей и синуса острого угла между ними является площадью четырехугольника. Рассмотрим пример расчета площади четырехугольника через диагональ.
Площадь участка сложной формы
- Причины для проведения расчета площади комнаты
- Площадь комнаты: проведение расчета площади пола
- Определение площади прямоугольной комнаты и потолка
- Какова площадь комнаты в которой имеются ниши и выступы
- Как определить площадь комнаты с неровными стенами
- Как высчитать площадь комнаты, в которой имеется многоуровневый потолок
- Определение общей площади комнаты
- Определение минимальной площади комнаты
- Оптимальная площадь комнаты
Причины для проведения расчета площади комнаты Существует большое количество причин, по которым определяется площадь стен, потолка или пола в помещении.
Площадь неправильного четырехугольника с заданными сторонами
Треугольник.
Площадь данного участка определяется путем умножения одной стороны треугольника на его высоту, то есть линию, опущенную с вершины треугольника, которая разделяет его на две равных части. Полученное значение удваивается. 3. Окружность или полуокружность. Определение радиуса. Данное значение переводится в квадрат, умножается на число Пи.
При наличии полукруга, значение разделяется на два. Кроме того, в интернете существуют специальные онлайн калькуляторы, позволяющие провести все расчеты быстро и качественно.
Для работы с ними достаточно выбрать форму участка комнаты, измерить его с помощью рулетки и ввести данные. Программа сама проведет все необходимые расчеты и определит площадь.
Оптимальная площадь комнаты Каждая комната имеет свой размер, и во время планировки дома, этот фактор учитывается в соответствии с их назначением.
Как вычислить площадь четырехугольника
Важно
Предпочтительно проводить замеры поближе к потолку, так как длина стены сверху и снизу помещения может отличаться. 2. Определите площадь пола по ранее указанным способам. 3. На каждом из вертикальных участков измерьте их высоту и длину и умножьте эти показатели.
4.
Прибавьте их к общему значению площади пола.
Определение общей площади комнаты Для того, чтобы ответить на вопрос как узнать площадь комнаты в квадратных метрах, предлагаем ознакомиться с инструкцией, которая поможет выполнить эту задачу: 1.
Позаботьтесь об очищении пространства возле стен. Стены комнаты должны быть в свободном доступе. Таким образом, повысится правильность и точность измерения.
Площадь земельного участка
Внимание
Игорь Воропаев — ведущий юрист «Проспер-Консалтинг»Консультант портала PropertyExperts Практически любой человек может Вам подсказать, что значит так называемая дачная система планировки.
Говоря об этой теме, стоит сразу сказать, что за величину мер участков принимаются не километры, и не метры, а сотки, гектары и погонные метры (например, не 10м, а 0,1га).
Именно погонные метры используют при расчете материала поверхности, к примеру, забора.
Считать просто: необходимо умножить на цену в рублях, и полученное значение будет равным минимальному количеству материалов, которое необходимо купить.
Точно также можно рассчитать, сколько будет использоваться грамм шпаклевки.
Измерять таким способом — простой и верный путь, и ничего больше спрашивать не нужно.
Площадь четырехугольника
Для того, чтобы определить площадь сегмента, который имеет форму прямоугольника с одинаковыми ребрами, достаточно измерить величину катетов, которые умножаются между собой и разделяются пополам.
То есть, для определения площади треугольного сегмента с катетами 0,5 и 0,9 м следует провести такие расчеты: 0,5х0,9/2= 0,225 метра квадратных. Как высчитать площадь комнаты, в которой имеется многоуровневый потолок Потолок, на котором имеются уступы рассчитать сложнее, однако вполне реально.
Существуют многоярусные потолки, которые имеют форму прямых линий их расчет проводить легко, но бывают такие конструкции, которые требуют особой внимательности, так как они состоят из дуго- или волнообразных фрагментов для расчета которых требуется приложить особые усилия.
Рассчитывать каждый из участков слишком долго и затратно, тем более, что в итоге получится не всегда правильный результат.
Источник: http://bk82.ru/kak-vyschitat-ploshhad-uchastka-esli-storony-raznye/
Вычислить площадь многоугольника онлайн
Формулы для вычисления площади выпуклого четырехугольника: ● S = 1 d1 d2 sin α 2 где S — площадь четырехугольника,d1, d2 — длины диагоналей четырехугольника,α — угол между диагоналями четырехугольника.
● S = p · r где S — площадь четырехугольника,p = a + b + c + d — полупериметр четырехугольника, 2 r — радиус вписанной окружности.
● S = √(p — a)(p — b)(p — c)(p — d) — abcd cos2θ где S — площадь четырехугольника,a, b, c, d — длины сторон четырехугольника,p = a + b + c + d — полупериметр четырехугольника, 2 θ = α + β — полусумма двух противоположных углов четырехугольника. 2 Вводить можно числа или дроби (-2.
4, 5/7, …). Более подробно читайте в правилах ввода чисел. Формулы площади геометрических фигур. Конвертер единиц расстояния и длины Конвертер единиц площади Присоединяйтесь © 2011-2017 Довжик Михаил Копирование материалов запрещено.
Важно
Мозган Онлайн калькулятор На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Через диагонали и угол между ними d1: ммсмм d2: ммсмм α: С°рад. Результат мм²см²м² Ответы: Формула для нахождения площади четырехугольников через диагонали и угол между ними: d1, d2 — диагонали; α — угол между диагоналями.
Через стороны и противолежащие углы a: ммсмм b: ммсмм c: ммсмм d: ммсмм α: С°рад.
β: С°рад.
Результат мм²см²м² Ответы: Формула для нахождения площади четырехугольников через стороны и противолежащие углы: p — полупериметр четырехугольника; a, b, c, d — стороны четырехугольника; α, β — противолежащие углы.
Результаты поиска
Внимание
4.
05 (46 ) Координаты многоугольника, разделенные пробелами Вы ввели следующие координаты многоугольника Площадь заданного многоугольника (в условных единицах) Описание Сервис позволяет высчитывать по заданным координатам вершин площадь многоугольника (треугольника, трапеции, паралеллограмма, пятиугольника и т.д) а также любых других непересекающихся многоугольников. Используется метод трапеций, суть которого заключается в том, что многоугольник представляет собой сумму трапеций, две вершины из которого это две соседние вершины многоугольника, а две другие вершины трапеции, есть абсциссы координат двух вершин многоугольника. Такой метод позволяет рассчитывать не только выпусклые многоугольники, но и любые другие, главное, что бы линии этого многоугольника не пересекались.
Площадь неправильного четырехугольника с заданными сторонами
β: С°рад.
Формулы
- P – периметр
- S – площадь
- R – радиус K
- r – радиус k
- n – количество сторон
- S’ – центр
- a – сторона
- K – окружность описанная
- k – окружность вписанная
При предоставлении услуг веб-сайт «Calculat.org» использует файлы куки.
Более информации Вы не любите рекламу? Мы ее тоже не любим, тем не менее доходы от рекламы предоставляют возможность функционирования нашего веб-сайта и бесплатного обслуживания наших посетителей. Пожалуйста, подумайте, не стоит ли отменить блокировку рекламы на этом веб-сайте.
Как рассчитать площадь четырехугольника
В онлайн калькуляте можно использовать величины в однаквых единицах измерения! Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади. Дополнительные возможности калькулятора вычисления площади четырехугольника
- Между полями для ввода можно перемещаться нажимая клавиши «вправо» и «влево» на клавиатуре.
Теория. Площадь четырехугольника Четырёхугольник — геометрическая фигура, состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки.
Четырёхугольник называется выпуклым, если отрезок соединяющий любые две точки этого четырехугольника, будет находиться внутри него.
Площадь и периметр многоугольника
С завидным упорством некоторые пользователи Planetcalc оставляют запросы на создание калькулятора для расчета площади неправильного четырехугольника, для которого известны только длины сторон.
Подумалось, что остановить их можно только написав вот такой шуточный калькулятор. (Нажмите кнопку «Остановить» для определения площади понравившегося Вам четырехугольника с заданными Вами сторонами).
12345678901234567890 Площадь фигуры: Четырехугольник: Площадь неправильного четырехугольника, зная только длины сторон, вычислить нельзя.
Калькулятор расчета площади земельного участка неправильной формы
DeutschEnglishEspañolFrançaisРусскийУкраїнська Используя этот онлайн калькулятор, вы сможете найти площадь четырехугольника.
Воспользовавшись онлайн калькулятором для вычисления площади четырехугольника, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.
Калькулятор Инструкция Теория Найти площадь четырехугольника Выберите известные величины:длины диагоналей и угол между нимидлины сторон и два противоположных углаполупериметр и радиус вписанной окружностиВведите данные: d1 = d2 = α = Ввод данных в калькулятор для вычисления площади четырехугольника В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел. N.B.
Источник: http://i-tb.ru/vychislit-ploshhad-mnogougolnika-onlajn/
sdelaydom.guru
Онлайн калькулятор: Площадь многоугольника
 Пример многоугольника
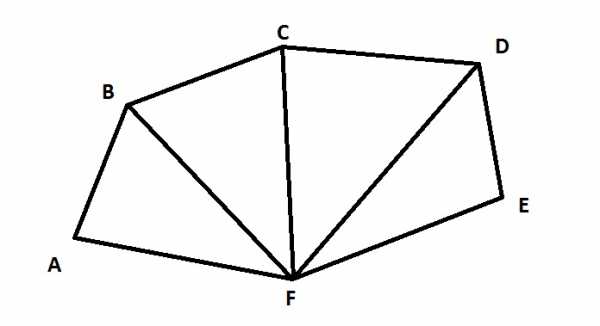
Пример многоугольникаДанный калькулятор обсчитывает площадь многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники.
Смотрим на картинку — площадь многоугольника ABCDE можно вычислить как сумму площадей треугольников ABD, BCD и ADE. Для этого, понятно, помимо длин сторон многоугольника, надо знать еще и длины диагоналей BD и AD, но это и все что нужно — площадь любого треугольника можно вычислить только по длинам его сторон, без измерения углов.
А это довольно удобно, например, при бытовом ремонте — длины-то всяко проще померять, чем углы.
Итак, измеряем длины сторон интересующего нас многоугольника, заносим их в таблицу, мысленно разбиваем многоугольник на треугольники, измеряем нужные диагонали, также заносим их в таблицу, после чего калькулятор рассчитывает площадь всей фигуры. Для проверки также выводятся площади обсчитанных им треугольников. В поле «Ошибка» выводится вершина, которую не удалось сопоставить ни одному треугольнику (если, например, введены еще не все диагонали).
По умолчанию в таблицу введены стороны и диагонали многоугольника на картинке, что легко исправить, нажав кнопку «Очистить таблицу».
Площадь многоугольника
addimport_exportmode_editdeleteСтороны и диагонали
Размер страницы: chevron_leftchevron_rightСтороны и диагонали
Сохранить ОтменитьИмпортировать данныеОшибка импорта
Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: ? EFGHIJKLMNOPQRSTUVWXYZ ?;50.5
Импортировать Назад Отменить Точность вычисленияЗнаков после запятой: 2
save Сохранить share Поделиться extension Виджет
planetcalc.ru
КАК ВЫЧИСЛИТЬ ПЛОЩАДЬ ЧЕТЫРЕХУГОЛЬНИКА — Вычисление площади четырехугольника
На примере расчета площади четырехугольника через диагонали понимаем, что формула очень похожа на расчет площади параллелограмма. Параллелограмм – это четырехугольник, у которого противоположные стороны равны и параллельны друг другу. Квадраты, прямоугольники и ромбы – это параллелограммы. Найти площадь квадрата можно найти по сторонам, площадь ромба легко вычисляется по диагоналям. В произвольном четырехугольнике также можно использовать все элементы для вывода формулы площади четырехугольника. Произвольный многоугольник с четырьмя углами встречается реже, чем его частные случаи, – трапеции, дельтоиды, параллелограммы. В последнюю «группу» входят также ромбы, прямоугольники, квадраты. Рассмотрим, какие данные фигуры необходимо знать, чтобы рассчитать ее площадь.
Понятие четырехугольник является общим названием для нескольких геометрических фигур. Это параллелограмм, прямоугольник, квадрат, ромб и трапеция. В произвольном четырехугольнике также можно использовать все элементы для вывода формулы площади четырехугольника. В школах и на экзаменах рассматриваются только выпуклые четырехугольники, так что поговорим о них. На среднем уровне образования изучают площади параллелограммов и трапеции. В случае же произвольного четырёхугольника все несколько сложнее, но также вполне доступно для среднего школьника. Ниже мы изучим различные методы расчётов площади произвольных четырёхугольников, запишем формулы и рассмотрим различные вспомогательные примеры. Мы помним, что периметр – это сумма длин всех сторон. Полупериметр – это половина периметра.
Начнем с четырехугольников. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности. Многоугольник численно характеризуется такой величиной, как площадь, которая показывает размер фигуры. Фигура, которая имеет три стороны, называется треугольником, а четыре — четырехугольником. Выпуклый многоугольник весь лежит относительно прямой (а она обязательно содержит какую-либо из его сторон) по одну сторону.
Из этой формулы вытекает Фо́рмула Брахмагу́пты, которая выражает площадь ВПИСАННОГО в окружность четырёхугольника как функцию длин его сторон. АннаАрт ее и применила, но в задании не сказано, что четырехугольник вписанный. Так как площадь треугольника равна 1/2absinC, где C – угол между сторонами a и b, вы можете найти площади двух треугольников и сложить их, чтобы вычислить площадь квадрата. Площадь прямоугольника равна произведению длины на ширину. Чтобы вычислить площадь прямоугольника, нужно знать его ширину (короткая сторона; представьте ее как высоту) и длину (длинная сторона; представьте ее как сторону, к которой проведена высота). Ниже я назову основные способы нахождения площадей треугольников и четырехугольников.
Еще интересное:
callbollonez.ru
Формула площади четырехугольника | Треугольники
Утверждение.
Площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними:
(d1, d2 — диагонали четырёхугольника, φ — угол между ними).
Дано: ABCD — выпуклый четырёхугольник,
AC∩BD=O, AC=d1, BD=d2, ∠AOB=φ
Доказать:
Доказательство:
Диагонали выпуклого четырёхугольника ABCD делят его на 4 треугольника.
Площадь каждого из треугольников равна половине произведения его сторон на синус угла между ними:
∠BOC=180°-∠AOB=180°-φ (как смежные).
∠COD=∠AOB=φ,
∠AOD=∠BOC=180°-φ (как вертикальные).
sin (180°-φ)=sin φ.
Отсюда
Таким образом,
Что и требовалось доказать.
Площади фигурwww.treugolniki.ru
Формула для расчета площади неправильного многоугольника
Конвертер единиц расстояния и длины Конвертер единиц площади Присоединяйтесь © 2011-2017 Довжик Михаил Копирование материалов запрещено. В онлайн калькуляте можно использовать величины в одинаквых единицах измерения! Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади. Дополнительные возможности калькулятора вычисления площади четырехугольника
- Между полями для ввода можно перемещаться нажимая клавиши «вправо» и «влево» на клавиатуре.
Теория. Площадь четырехугольника Четырёхугольник — геометрическая фигура, состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Четырёхугольник называется выпуклым, если отрезок соединяющий любые две точки этого четырехугольника, будет находиться внутри него.
Как узнать площадь многоугольника?
Формула определения площади определяется путем взятия каждого ребра многоугольника АВ, и вычисления площади треугольника АВО с вершиной в начале координат О, через координаты вершин. При обходе вокруг многоугольника, образуются треугольники, включающие внутреннюю часть многоугольника и расположенные снаружи его. Разница между суммой этих площадей и есть площадь самого многоугольника.
Поэтому формула называется формулой геодезиста, так как «картограф» находится в начале координат; если он обходит участок против часовой стрелки, площадь добавляется если она слева и вычитается если она справа с точки зрения из начала координат. Формула площади действительна для любого самонепересекающегося (простого) многоугольника, который может быть выпуклым или вогнутым. Содержание
- 1 Определение
- 2 Примеры
- 3 Более сложный пример
- 4 Объяснение названия
- 5 См.
Площадь многоугольника
Внимание Это может быть:- треугольник;
- четырехугольник;
- пяти- или шестиугольник и так далее.
Такая фигура непременно будет характеризоваться двумя положениями:
- Смежные стороны не принадлежат одной прямой.
- У несмежных отсутствуют общие точки, то есть они не пересекаются.
Чтобы понять, какие вершины являются соседними, потребуется посмотреть, принадлежат ли они одной стороне. Если да, то соседние. В противном случае их можно будет соединить отрезком, который необходимо назвать диагональю. Их можно провести только в многоугольниках, у которых больше трех вершин.
Какие их виды существуют? Многоугольник, у которого больше четырех углов, может быть выпуклым или вогнутым. Отличие последнего в том, что некоторые его вершины могут лежать по разные стороны от прямой, проведенной через произвольную сторону многоугольника.
Как найти площадь правильного и неправильного шестиугольника?
- Зная длину стороны, умножим её на 6 и получим периметр шестиугольника:10 см х 6 = 60 см
- Подставим полученные результаты в нашу формулу:
- Площадь = 1/2*периметр*апофему Площадь = ½*60см*5√3 Решаем: Теперь осталось упростить ответ, чтобы избавиться от квадратных корней, а полученный результат укажем в квадратных сантиметрах: ½ * 60 см * 5√3 см =30 * 5√3 см =150 √3 см =259.8 см² Видео о том, как найти площадь правильного шестиугольника Существует несколько вариантов определения площади неправильного шестиугольника:
- Метод трапеции.
- Метод расчета площади неправильных многоугольников при помощи оси координат.
- Метод разбивания шестиугольника на другие фигуры.
В зависимости от исходных данных, которые вам будут известны, подбирается подходящий метод.
Некоторые неправильные шестиугольники состоят из двух параллелограммов. Для определения площади параллелограмма следует умножить его длину на ширину и затем сложить две уже известные площади. Видео о том, как найти площадь многоугольника Равносторонний шестиугольник имеет шесть равных сторон и является правильным шестиугольником.
Площадь равностороннего шестиугольника равняется 6 площадям треугольников, на которые разбита правильная шестиугольная фигура. Все треугольники в шестиугольнике правильной формы равны, поэтому для нахождения площади такого шестиугольника достаточно будет знать площадь хотя бы одного треугольника. Для нахождения площади равностороннего шестиугольника используется, конечно же, формула площади правильного шестиугольника, описанная выше.
404 not found
Украшение жилища, одежды, рисование картин способствовало процессу формирования и накопления сведений в области геометрии, которые люди тех времён добывали опытным путем, по крупицам и передавали из поколения в поколение. Сегодня знания геометрии необходимы и закройщику, и строителю, и архитектору и каждому простому человеку в быту. Поэтому нужно учиться рассчитывать площадь различных фигур, и помнить, что каждая из формул может пригодиться впоследствии на практике, в том числе, и формула правильного шестиугольника.
Шестиугольником называется такая многоугольная фигура, общее количество углов которой равно шести. Правильным шестиугольником называют шестиугольную фигуру, которая имеет равные стороны. Углы у правильного шестиугольника также между собой равны.
В повседневной жизни мы часто можем встретить предметы, имеющие форму правильного шестиугольника.
Калькулятор площади неправильного многоугольника по сторонам
Вам понадобится
- — рулетка;
- — электронный дальномер;
- — лист бумаги и карандаш;
- — калькулятор.
Инструкция 1 Если вам нужна общая площадь квартиры или отдельной комнаты, просто прочтите технический паспорт на квартиру или дом, там указан метраж каждого помещения и общий метраж квартиры. 2 Для измерения площади прямоугольной или квадратной комнаты возьмите рулетку или электронный дальномер и измерьте длину стен. При измерении расстояний дальномером обязательно следите за перпендикулярностью направления луча, иначе результаты замеров могут быть искажены. 3 Затем полученную длину (в метрах) комнаты умножьте на ширину (в метрах). Полученное значение и будет площадью пола, она измеряется в квадратных метрах.
Формула площади гаусса
Если требуется посчитать площадь пола более сложной конструкции, например, пятиугольной комнаты или комнаты с круглой аркой, схематично начертите эскиз на листе бумаги. Затем разделите сложную форму на несколько простых, например, на квадрат и треугольник или прямоугольник и полукруг. Измерьте при помощи рулетки или дальномера величину всех сторон получившихся фигур (для круга необходимо узнать диаметр) и занесите результаты на ваш чертеж.
5 Теперь посчитайте площадь каждой фигуры по отдельности. Площадь прямоугольников и квадратов высчитывайте перемножением сторон. Для расчета площади круга диаметр разделите пополам и возведите в квадрат (умножьте его на самого себя), затем умножьте полученное значение на 3,14.
Если вам нужна только половина круга, разделите полученную площадь пополам. Чтобы рассчитать площадь треугольника, найдите Р, для этого сумму всех сторон поделите на 2.
Формула расчета площади неправильного многоугольника
Если точки пронумерованы последовательно в направлении против часовой стрелки, то детерминанты в формуле выше положительны и модуль в ней может быть опущен; если они пронумерованы в направлении по часовой стрелке, детерминанты будут отрицательными. Это происходит потому, что формула может рассматриваться как частный случай теоремы Грина. Для применения формулы необходимо знать координаты вершин многоугольника в декартовой плоскости.
Для примера возьмём треугольник с координатами {(2, 1), (4, 5), (7, 8)}. Возьмём первую х -координату первой вершины и умножим её на y -координату второй вершины, а затем умножим х второй вершины на y третьей. Повторим эту процедуру для всех вершин. Результат может быть определен по следующей формуле:[3] A tri.
Формула расчета площади неправильного четырехугольника
A} _{\text{tri.}}={1 \over 2}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3}|} где xi и yi обозначают соответствующую координату. Эту формулу можно получить, раскрыв скобки в общей формуле для случая n = 3. По этой формуле можно обнаружить, что площадь треугольника равна половине суммы 10 + 32 + 7 − 4 − 35 − 16, что даёт 3. Число переменных в формуле зависит от числа сторон многоугольника. Например, в формуле для площади пятиугольника будут использоваться переменные до x5 и y5: A pent. = 1 2 | x 1 y 2 + x 2 y 3 + x 3 y 4 + x 4 y 5 + x 5 y 1 − x 2 y 1 − x 3 y 2 − x 4 y 3 − x 5 y 4 − x 1 y 5 | {\displaystyle \mathbf {A} _{\text{pent.}}={1 \over 2}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{5}+x_{5}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{5}y_{4}-x_{1}y_{5}|} A для четырехугольника — переменные до x4 и y4: A quad.
1privilege.ru
Как рассчитать площадь неправильного многоугольника с разными сторонами
К примеру, правильный пятиугольник называется пентагон, шести — гексагон, восьмиугольник — октагон, десятиугольник — декагон, одиннадцатиугольник — гендекагон, двенадцати — додекагон. Любой правильный многоугольник имеет свою вписанную и описанную окружность. При этом круг также можно представить как правильный полигон, который имеет бесконечное количество углов. Многоугольники в реальности Невыпуклые многоугольники практически не распространены в реальной жизни: они довольно редко встречаются в природе, а в рукотворном виде она выступают в роли граней деталей машин. Многие морские организмы обладают пентасимметрией, и наиболее очевидным примером невыпуклой фигуры является морская звезда. Правильные геометрические фигуры наоборот широко встречаются в природе. Наиболее очевидным примером являются пчелиные соты, каждая ячейка которых представляет собой гексагон.
Площадь многоугольника
- Зная длину стороны, умножим её на 6 и получим периметр шестиугольника:10 см х 6 = 60 см
- Подставим полученные результаты в нашу формулу:
- Площадь = 1/2*периметр*апофему Площадь = ½*60см*5√3 Решаем: Теперь осталось упростить ответ, чтобы избавиться от квадратных корней, а полученный результат укажем в квадратных сантиметрах: ½ * 60 см * 5√3 см =30 * 5√3 см =150 √3 см =259.8 см² Видео о том, как найти площадь правильного шестиугольника Существует несколько вариантов определения площади неправильного шестиугольника:
- Метод трапеции.
- Метод расчета площади неправильных многоугольников при помощи оси координат.
- Метод разбивания шестиугольника на другие фигуры.
В зависимости от исходных данных, которые вам будут известны, подбирается подходящий метод.
Шаг 1: Найдем площадь.Площадь = ((длина стороны)² * N) / (4Tan(π / N))= ((2)² * 4) / (4 * Tan(3.14 / 4))= (4 * 4) / 4 * Tan(0.785)= 16 / 4 * 0.999= 16 / 3.996Площадь = 4. Шаг 2: Найдем периметр.Периметр = (N * (длина стороны) = 4 * 2 = 8 Задача 2: Найдите площадь и периметр многоугольника, если радиус описанной окружности = 2, количество сторон многоугольника = 5.
Шаг 1: Найдем площадь.Площадь = ½ * R² * Sin(2π / N)= (0.5) * 2² * Sin(2 * 3.14 / 5)= 0.5 * 4 * Sin(6.28 / 5)= 2 * Sin(1.26)= 2 * 0.95Площадь = 1.9. Задача 3:Найдите площадь многоугольника с радиусом описанной окружности равному 2 и количеству сторон 5, используя радиус вписанного круга.
Как посчитать площадь многоугольника
На нашем сайте пользователи инж енеров в обл асти ф изики, химической, электрической, эле ктроника, Строительство и гражданских, оптики и лазерн ой, механической, финансов, нефти и газа, структурных и т. Даже несколько средних школ исп ользует наш сайт в свои учебные пр ограммы и препод авать вПравильный многоугольник = (A * P) / 2 где A = сторона / (2 * Tan(π / N))
- R = Радиус описанной окрудности,
- A = Радиус вписанного круга,
- P = Периметр
- N = Количество сторон,
Задача 1 : Найдите и периметр многоугольника, если длина стороны = 2 и количество = 4.
Шаг 1: Найдем. = ((длина стороны)² * N) / (4Tan(π / N)) Шаг 2: Найдем периметр.
Правильный многоугольник
Если форму многоугольника имеет фигура очень большой площади, например, земельный участок, провести отрезки необходимой длины будет довольно-таки проблематично. Поэтому, в таком случае поступите следующим образом: вбейте в центр многоугольника колышек и протяните от него к каждой вершине отрезок бечевки.
Затем измерьте и запишите в строгой последовательности длины всех отрезков. Аналогичным образом измерьте и стороны самого многоугольника, натянув бечевку между соседними вершинами.
4 Чтобы воспользоваться формулой Герона, сначала посчитайте полупериметр каждого треугольника по формуле: р = ½ * (а + b + с), где:а, b и c – длины сторон треугольника,р – полупериметр (стандартное обозначение). Определив полупериметр треугольника, подставьте полученное число в следующую формулу: S∆ = √(р*(p-a)*(p-b)*(p-c)), где:S∆ – площадь треугольника.
5 Если многоугольник выпуклый, т.е.
Как узнать площадь многоугольника?
Инфо Определив полупериметр треугольника, подставьте полученное число в следующую формулу:- — бечевка;
- — рулетка;
- — циркуль;
- — линейка;
- — калькулятор.
а, b и c – длины сторон треугольника, р – полупериметр (стандартное обозначение). Как рассчитать площадь четырехугольника На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн.
Для расчета задайте длину, длины диагоналей и угол между ними, противолежащие углы, радиус окружности. Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (), попарно соединяющих эти точки.
Как посчитать площадь неправильного многоугольника
Через диагонали и угол между ними Формула для нахождения четырехугольников через диагонали и угол между ними: Через стороны и противолежащие углы Формула для нахождения площади четырехугольников через стороны и противолежащие углы: вписанного четырехугольника в окружность Формула Брахмагупты для нахождения вписанного четырехугольника в окружность: Площадь описанного четырехугольника около окружности через радиус Формула для нахождения описанного четырехугольника около окружности через радиус: описанного четырехугольника около окружности через и противолежащие углы Формула для нахождения площади описанного четырехугольника около окружности через стороны и противолежащие углы: Как посчитать площадь неправильного многоугольника где а — его сторона. квадрата можно также вычислить по формуле где — диагональ квадрата.
Калькулятор площади многоугольника
Вам понадобится
- — бечевка;
- — рулетка;
- — циркуль;
- — линейка;
- — калькулятор.
Инструкция 1 Чтобы посчитать площадь произвольного многоугольника, отметьте внутри него произвольную точку, а затем соедините ее с каждой вершиной. Если многоугольник невыпуклый, выберите точку таким образом, чтобы проведенные отрезки не пересекали стороны фигуры.
Например, если многоугольник является внешней границей «звезды», то точку нужно отметить не в «луче» звезды, а в ее центре. 2 Теперь измерьте длины сторон в каждом из образовавшихся треугольников. После этого воспользуйтесь формулой Герона и вычислите площадь каждого из них.
Сумма площадей всех треугольников и будет искомой площадью многоугольника.
Калькулятор расчета площади земельного участка неправильной формы
В этом случае, треугольников получится на два меньше, что иногда может существенно упростить задачу нахождения площади многоугольника. Система расчета площадей полученных треугольников не отличается от описанной выше.
6 При решении школьных задач и «задач на смекалку» внимательно рассмотрите форму многоугольника. Возможно, его удастся разбить на несколько частей, из которых можно будет сложить «правильную» фигуру, например, квадрат. 7 Иногда многоугольник можно «дополнить» до правильной фигуры. В таком случае, просто вычтите из площади дополненной фигуры площадь дополнения.
Кстати, этот способ актуален не только для решения абстрактных задач.
Как найти площадь правильного и неправильного шестиугольника?
Расчет площади Многоугольника, используя радиус вписанного круга и длину стороны:[ (A×P)/2 ][ Apothem(A) = side/(2×Tan(π/N)) ] Введите длину = Введите кол-во сторон = Площадь Многоугольника = Расчет площади по длине стороны:Площадь Многоугольника = ((side)² * N) / (4Tan(π / N))Периметр Многоугольника = N * (side) Расчет площади по радиусу описанной окружности :Площадь Многоугольника = ½ * R² * Sin(2π / N) Расчет площади по радиусу вписанного круга :Площадь Многоугольника = A² * N * Tan(π / N)где, A = R * Cos(π / N) По радиусу вписанного круга и длине стороны :Площадь Многоугольника = (A * P) / 2где A = сторона / (2 * Tan(π / N))где,
- N = Количество сторон,
- A = Радиус вписанного круга,
- R = Радиус описанной окрудности,
- P = Периметр
Примеры: Задача 1: Найдите площадь и периметр многоугольника, если длина стороны = 2 и количество сторон = 4.
Некоторые неправильные шестиугольники состоят из двух параллелограммов. Для определения площади параллелограмма следует умножить его длину на ширину и затем сложить две уже известные площади.
Видео о том, как найти площадь многоугольника Равносторонний шестиугольник имеет шесть равных сторон и является правильным шестиугольником. Площадь равностороннего шестиугольника равняется 6 площадям треугольников, на которые разбита правильная шестиугольная фигура.
Все треугольники в шестиугольнике правильной формы равны, поэтому для нахождения площади такого шестиугольника достаточно будет знать площадь хотя бы одного треугольника. Для нахождения площади равностороннего шестиугольника используется, конечно же, формула площади правильного шестиугольника, описанная выше.
В задачах по геометрии часто требуется вычислить площадь многоугольника. Причем он может иметь довольно разнообразную форму – от всем знакомого треугольника до некоторого n-угольника с каким-то невообразимым числом вершин. К тому же эти многоугольники бывают выпуклыми или вогнутыми. В каждой конкретной ситуации полагается отталкиваться от внешнего вида фигуры. Так получится выбрать оптимальный путь решения задачи. Фигура может оказаться правильной, что существенно упростит решение задачи.
Немного теории о многоугольниках Если провести три или более пересекающихся прямых, то они образуют некоторую фигуру. Именно она является многоугольником. По количеству точек пересечения становится ясно, сколько вершин у него будет.
Они дают название получившейся фигуре.
adler-group.ru