Как найти площадь геометрических фигур? – boeffblog.ru
Что такое площадь?
Площадь – характеристика замкнутой геометрической фигуры (круг, квадрат, треугольник и т.д.), которая показывает ее размер. Площадь измеряется в квадратных сантиметрах, метрах и т.д. Обозначается буквой S (square).
Как найти площадь треугольника?
1. Самая известная формула площади треугольника по стороне и высоте:
S = a · h
где a – длина основания, h – высота треугольника, проведенная к основанию.
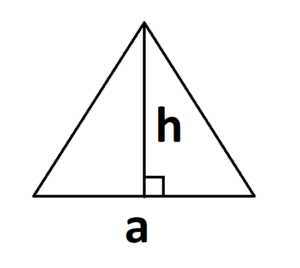
Причем, основание не обязательно должно находиться снизу. Так тоже сойдет. 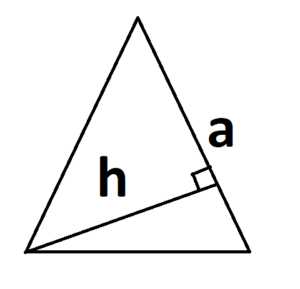
Если треугольник тупоугольный, то высота опускается на продолжение основания:
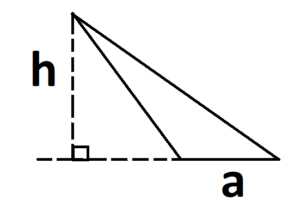
Если треугольник прямоугольный, то основанием и высотой являются его катеты:
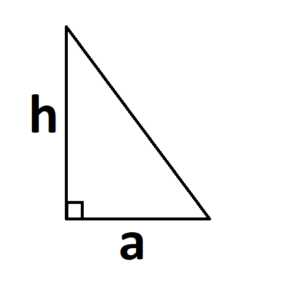
2. Другая формула, которая является не менее полезной, но которую почему-то всегда забывают:
S = a · b · sinα
где a и b – две стороны треугольника, sinα – синус угла между этими сторонами.
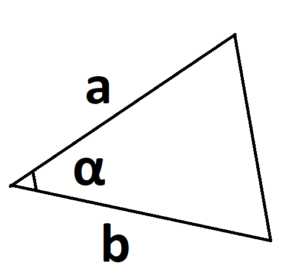
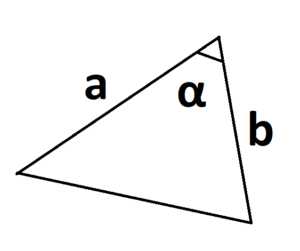
Главное условие – угол берется между двумя известными сторонами.
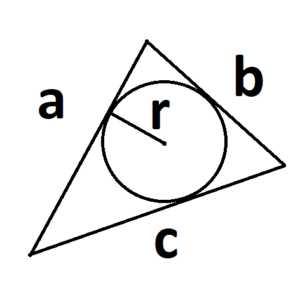
3. Формула площади по трем сторонам (формула Герона):
S =
где a, b и с – стороны треугольника, а р – полупериметр. p = ( a + b + c)/2.
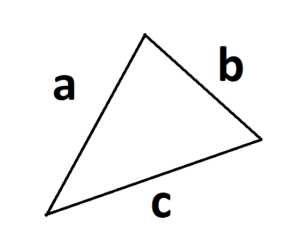
4. Формула площади треугольника через радиус описанной окружности:
S =
где a, b и с – стороны треугольника, а R – радиус описанной окружности.
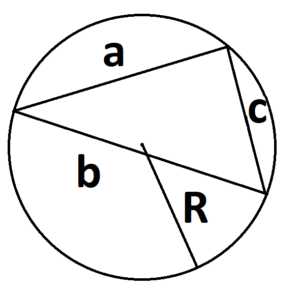
5. Формула площади треугольника через радиус вписанной окружности:
S =p · r
где р – полупериметр треугольника, а r – радиус вписанной окружности.
Как найти площадь прямоугольника?
1. Площадь прямоугольника находится довольно-таки просто:
S = a · b
Никаких подвохов.
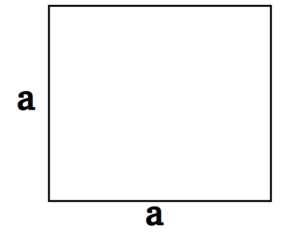
Как найти площадь квадрата?
1. Так как квадрат является прямоугольником, у которого все стороны равны, то к нему применяется такая же формула:
S = a · a = a2
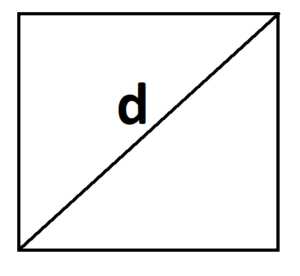
2. Также площадь квадрата можно найти через его диагональ:
S = d2
Как найти площадь параллелограмма?
1. Площадь параллелограмма находится по формуле:
S = a · h
Это связано с тем, что если от него отрезать прямоугольный треугольник справа и приставить его слева, получится прямоугольник:
2. Также площадь параллелограмма можно найти через угол между двумя сторонами:
S = a · b · sinα
Как найти площадь ромба?
Ромб по своей сути является параллелограммом, у которого все стороны равны. Поэтому для него применяются те же формулы площади.
1. Площадь ромба через высоту:
S = a · h
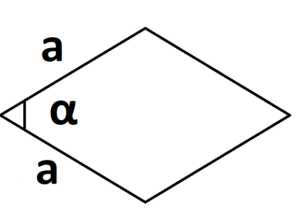
2. Площадь ромба через угол между сторонами:
S = a · a sinα = a2 · sinα
3. Площадь ромба через диагонали:
S = d1 · d2
Как найти площадь трапеции?
1. Площадь трапеции находится по следующей формуле:
S = · h
Как найти площадь круга?
1. Площадь круга можно найти через радиус:
S = π r2
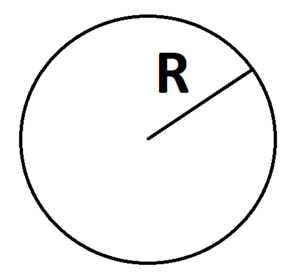
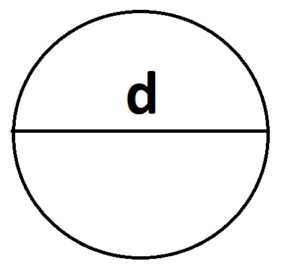
2. Площадь круга можно найти через диаметр:
S =
πd2/4
boeffblog.ru
Площадь треугольника. Онлайн-калькулятор
Онлайн-калькулятор для расчета площади треугольника поможет Вам найти площадь треугольника несколькими способами в зависимости от известных данных. Наш калькулятор не просто рассчитает площадь треугольника, но и покажет подробное решение, которое будет показано под калькулятором. Поэтому данный калькулятор удобно использовать не только для быстрых расчетов, но и для проверки своих вычислений. С помощью данного калькулятора вы сможете найти площадь треугольника по следующим формулам: через основание и высоту, через две стороны и угол, по трем сторонам (формула Герона), через радиус вписанной окружности, через радиус описанной окружности.
Рассчитать
Треугольник – это геометрическая фигура, которая образована тремя отрезками. Эти отрезки называются сторонами треугольниками, а точки соединения отрезков – вершинами треугольника. В зависимости от соотношения сторон треугольники бывают нескольких видов: равнобедренный треугольник (две стороный треугольника равны между собой, эти стороны называются боковыми сторонами, а третья сторона называется основанием треугольника), равносторонний треугольник (у треугольника все три стороны равны), прямоугольный треугольник (один угол треугольника прямой).
Как найти площадь треугольника?
Найти площадь треугольника очень просто, достаточно воспользоваться нашим калькулятором или рассчитать самостоятельно, воспользовавшись формулой площади треугольника. В зависимости от того, какие данные известны, для расчета площади треугольника использует несколько способов:
1) через основание и высоту
a – основание треугольника,h – высота треугольника.
2) через две стороны и угол
a, b – стороны треугольника,α – угол между сторонами.
3) По трем сторонам. Формула Герона.
a, b, с – стороны треугольника,p – полупериметр треугольника.
4) Через радиус вписанной окружности.
a, b, с – стороны треугольника,p – полупериметр треугольника,
r – радиус вписанной окружности.
5) Через радиус описанной окружности.
a, b, с – стороны треугольника,R – радиус описанной окружности.
Вы всегда сможете проверить правильность расчета площади треугольника с помощью нашего калькулятора.
Формулы геометрии. Площади фигур. — материалы для подготовки к ЕГЭ по Математике
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
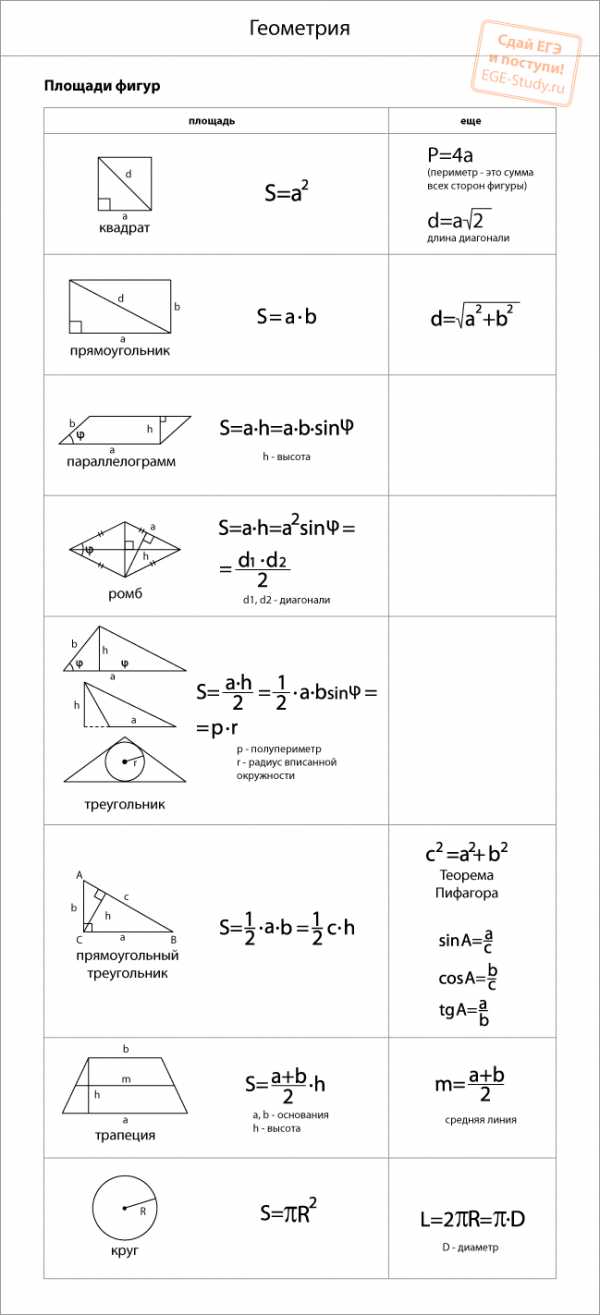
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
Ты нашел то, что искал? Поделись с друзьями!
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
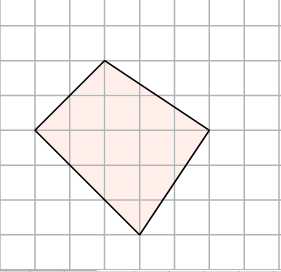
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
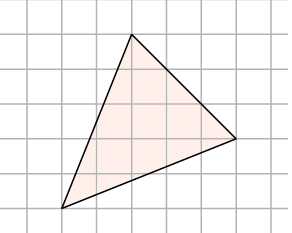
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
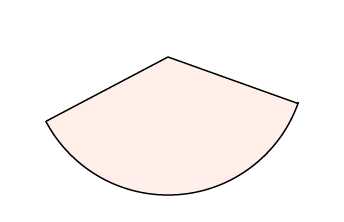
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Ответ: .
Читайте также о задачах на тему «Координаты и векторы». Для их решения вспомните, что такое абсцисса точки (это ее координата по ) и что такое ордината (координата по ). Пригодятся также такие понятия, как координаты вектора и длина вектора (она находится по теореме Пифагора), синус и косинус угла, угловой коэффициент прямой, уравнение прямой, а также сумма, разность и скалярное произведение векторов, угол между векторами.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Задачи на нахождение площади. Математика 4 класс.
Задача 1
Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?
Решение:
- 1) 8 ∙ 7 = 56
- Ответ: Площадь прямоугольника 56 м².
Задача 2
Площадь витрины квадратной формы 64м². Узнай ее периметр.
Решение:
- 1) 1) 64 : 8 = 8 (сторна витрины)
- 2) 2) 8 ∙ 4 = 32 (периметр витрины)
- Ответ: 32 м.
Задача 3
Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.
Решение:
- 1) 1) 90 ∙ 7 = 630
- Ответ: 630 см².
Задача 4
Два прямоугольных участка имеют одинаковую площадь. Длина первого — 48 м, а ширина 30 м. Чему равна длина второго участка, если его ширина на 6 м больше ширины первого участка?
Решение:
- 1) 48 ∙ 30 = 1440 (площадь первого участка)
- 2) 30 + 6 = 36 (ширина второго участка)
- 3) 1440 : 36 = 40
- Ответ: длина второго участка 40 м.
Задача 5
Один прямоугольный участок имеет длину 36 м, а ширину 20 м. Найдите ширину другого участка с такой же площадью, если его длина на 6 м меньше длины первого участка.
Решение:
- 1) 36 ∙ 20 = 720 (площадь первого участка)
- 2) 36 – 6 = 30 (длина другого участка)
- 3) 720 : 30 = 24
- Ответ: ширина другого участка 24 м.
Задача 6
У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?
Решение:
- 1) 4 ∙ 4 = 16 (площадь квадрата)
- 2) 2 ∙ 6 = 12 (площадь прямоугольника)
- 3) 16 — 12 = 4
- Ответ: площадь квадратата больше на 4 см.
Задача 7
Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
Решение:
- 1) 6 ∙ 6 = 36
- 2) 6 ∙ 4 = 24
- Ответ: площадь квадрата 36 см², периметр квадрата 24 см.
Задача 8
У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
Решение:
- 1) 7 ∙ 5 = 35
- 2) 7 ∙ 2 = 14
- 3) 5 ∙ 2 = 10
- 4) 10 + 14 = 24
- Ответ: площадь прямоугольника 35 м², периметр прямоугольника 24 см.
Задача 9
Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?
Решение:
- 1) 8 ∙ 8 = 64 (площадь клумбы)
- 2) 64 : 16 = 4(1/16 клумбы)
- 3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
- 4) 64 – 28 = 36
- Ответ: незабудками засажено 36 м².
Задача 10
Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?
Решение:
- 1) 6 ∙ 2 = 12
- 2) 18 – 12 = 6
- 3) 6 : 2 = 3 (ширина прямоугольника)
- 4) 3 ∙ 6 = 18
- Ответ: площадь прямоугольника 18 м².
Задача 11
Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?
Решение:
- 1) 4800 : 60 = 80 (длина стола)
- 2) 60 ∙ 2 = 120 см
- 3) 80 ∙ 2 = 160 см
- 4) 120 + 160 = 280 см
- Ответ: периметр стола 280 см.
Задача 12
Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?
Решение:
- 1) 5 ∙ 2 = 10
- 2) 40 – 10 = 30
- 3) 30 : 2 = 15 (другая сторона прямоугольника)
- 4) 5 ∙ 15 = 75
- Ответ: площадь прямоугольника 75 см².
Задача 13
Площадь квадрата 49 кВ дм. Узнайте его периметр.
Решение:
- 1) 49 : 7 = 7 (сторона квадрата)
- 2) 7 ∙ 4 = 28 (периметр квадрата)
- Ответ: периметр квадрата равен 28 дм.
Задача 14
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.
Решение:
- 1) 4 ∙ 2 = 8 (длина окна)
- 2) 4 ∙ 8 = 32
- Ответ: площадь окна равна 32 м².
Задача 15
Длина участка земли 54 м. ширина — 48 м. 5/9 площади засажено картофелем. Остальная часть участка – капустой. Какая площадь засажена капустой?
Решение:
- 1) 54 ∙ 48 = 2592 (площадь участка земли)
- 2) 2592 : 9 = 288 (1/9 площади)
- 3) 288 ∙ 5 = 1440 (5/9 площади)
- 4) 2592 – 1440 = 1152
- Ответ: капустой засадили 1152 м².
mat-zadachi.ru
Метод площадей для решения задач
\(\blacktriangleright\) Теорема 1. Если вершину треугольника перемещать по прямой, параллельной противолежащей стороне, то площадь при этом останется прежней.
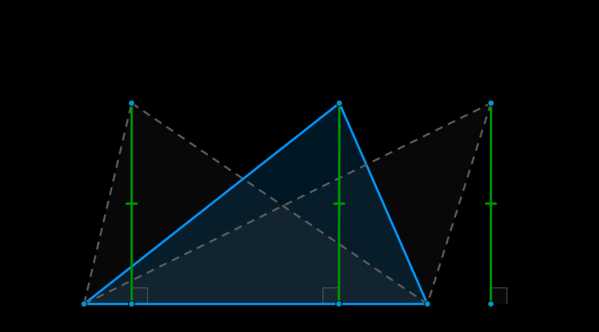
Доказательство: Рассмотрим три треугольника \(\triangle ABC, \triangle A_1BC, \triangle A_2BC\). Т.к. \(A_1A_2\parallel BC\), то расстояние от любой точки одной из этих прямых до другой прямой одинаково. То есть высоты, опущенные из точек \(A, A_1, A_2\) на прямую \(BC\) будут равны: \(AH=A_1H_1=A_2H_2=h\). Т.к. у этих треугольников общее основание \(BC\), то: \[S_{\triangle ABC}=S_{\triangle A_1BC}=S_{\triangle A_2BC}=\dfrac12BC\cdot h\]
\(\blacktriangleright\) Теорема 2. Если два треугольника имеют равные высоты (общую высоту), то их площади относятся как основания, к которым эти высоты проведены.
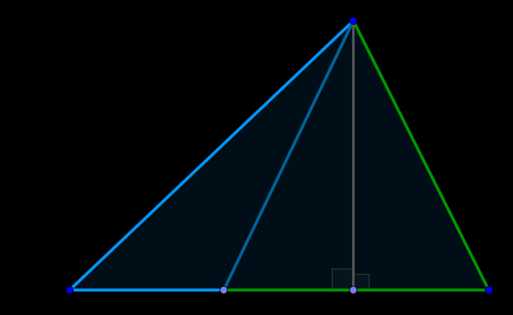
Доказательство: Рассмотрим треугольники \(\triangle ABC\) и \(\triangle ABC_1\): т.к. высота треугольника — это перпендикуляр, опущенный из вершины на прямую, содержащую противолежащую сторону, то \(AH\) — высота и \(\triangle ABC\), и \(\triangle ABC_1\). Следовательно: \[\dfrac{S_{\triangle ABC}}{S_{\triangle ABC_1}}=\dfrac{\frac12 AH\cdot BC}{\frac12 AH\cdot BC_1}=\dfrac{BC}{BC_1}\]
\(\blacktriangleright\) Теорема 3. Если два треугольника имеют одинаковые стороны (общую сторону), то их площади относятся как высоты, которые к этим сторонам проведены.
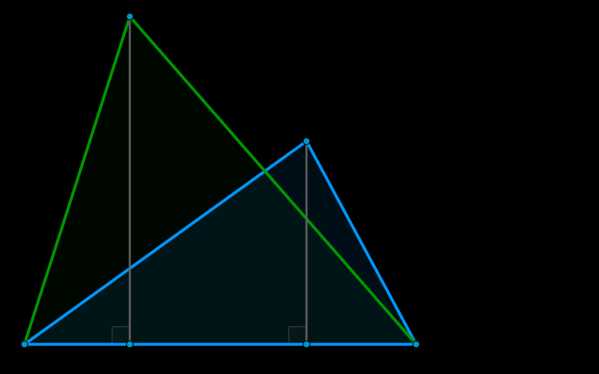
Доказательство: Рассмотрим треугольники \(\triangle ABC\) и \(\triangle ABC_1\). Проведем на их общую сторону \(AB\) высоты \(CH\) и \(C_1H_1\). Тогда: \[\dfrac{S_{\triangle ABC}}{S_{\triangle ABC_1}}=\dfrac{\frac12 CH\cdot AB}{\frac12 C_1H_1\cdot AB}=\dfrac{CH}{C_1H_1}\]
\(\blacktriangleright\) Следствие: Медиана треугольника делит его на два треугольника, равных по площади.
Доказательство: по теореме 2 площади \(\triangle ABM\) и \(\triangle CBM\) относятся как основания \(AM\) и \(CM\). Но \(AM=CM \Rightarrow S_{\triangle ABM}=S_{\triangle CBM}\).
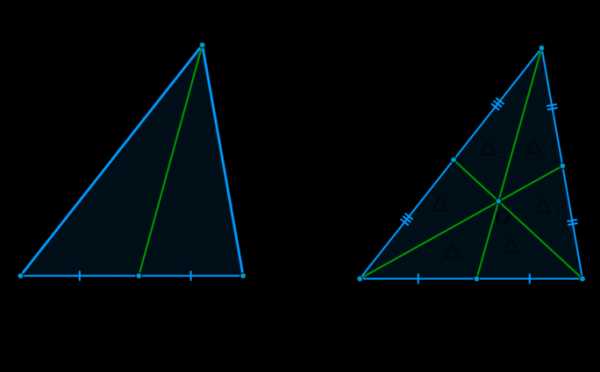
\(\blacktriangleright\) Следствие: Все три медианы треугольника делят его на шесть треугольников, равных по площади.
Доказательство: т.к. \(AK\) — медиана \(\triangle ABC\), то \(S_{\triangle_1}+S_{\triangle_2}+S_{\triangle_3}=S_{\triangle_4}+S_{\triangle_5}+S_{\triangle_6}\).
Т.к. \(OK\) — медиана \(\triangle OBC\), то \(S_{\triangle_3}=S_{\triangle_4}\). Следовательно, \(S_{\triangle_1}+S_{\triangle_2}=S_{\triangle_5}+S_{\triangle_6} \ (*)\).
Т.к. \(ON\) — медиана \(\triangle AOB\), то \(S_{\triangle_1}=S_{\triangle_2}\), аналогично, \(S_{\triangle_5}=S_{\triangle_6}\). Следовательно, подставляя эти равенства в \((*)\), получим: \(2S_{\triangle_1}=2S_{\triangle_6} \Rightarrow S_{\triangle_1}=S_{\triangle_6} \Rightarrow S_{\triangle_2}=S_{\triangle_5}\).
Аналогично доказывается, что \(S_{\triangle_4}=S_{\triangle_5}\). Таким образом, площади всех этих треугольников равны.
\(\blacktriangleright\) Теорема 4. Если два треугольника имеют по равному углу (общему углу), то их площади относятся как произведения сторон, образующих эти углы.
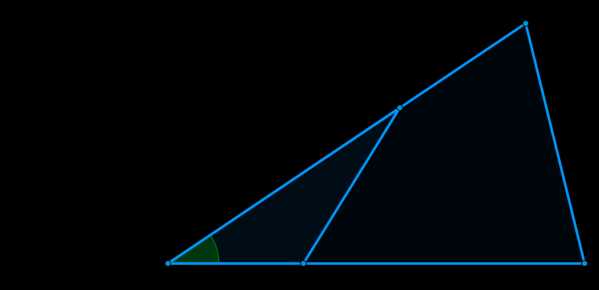
Доказательство: Рассмотрим треугольники \(\triangle B_1AC_1\) и \(\triangle BAC\), имеющие равный (общий) \(\angle A\). Т.к. площадь треугольника равна полупроизведению сторон на синус угла между ними, то: \[\dfrac{S_{\triangle BAC}}{S_{\triangle B_1AC_1}}=\dfrac{\frac12 \sin \angle A\cdot BA\cdot AC}{\frac12 \sin \angle A\cdot B_1A\cdot AC_1}=\dfrac{BA\cdot AC}{B_1A\cdot AC_1}\]
\(\blacktriangleright\) Следствие: Биссектриса угла треугольника делит его на два треугольника, площади которых относятся как стороны, образующие этот угол.
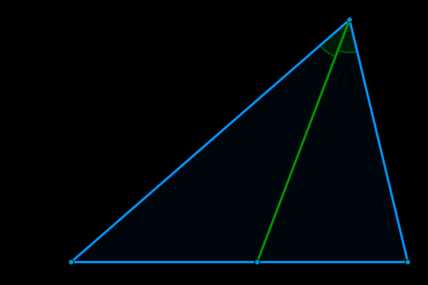
Доказательство: \(\dfrac{S_{\triangle ABR}}{S_{\triangle CBR}}=\dfrac{\frac12 \sin \alpha \cdot AB\cdot BR}{\frac12 \sin \alpha\cdot CB\cdot BR}=\dfrac{AB}{CB}\)
\(\blacktriangleright\) Теорема 5. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
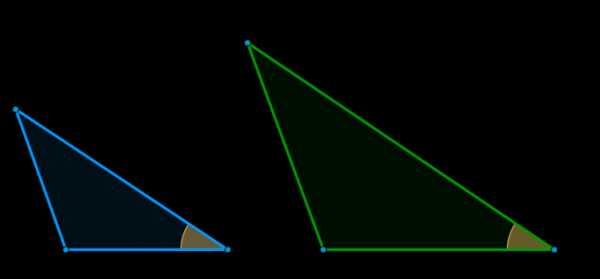
Доказательство: т.к. треугольники подобны, то все стороны одного треугольника в \(k\) раз больше всех сторон другого, а углы между сходственными сторонами равны. Значит, \[\dfrac{S_{\triangle ABC}}{S_{\triangle A_1B_1C_1}}=\dfrac{\frac12 \sin \angle C\cdot BC\cdot AC}{\frac12 \sin \angle C_1\cdot B_1C_1\cdot A_1C_1}=\dfrac{ka\cdot kb}{a\cdot b}=k^2\]
\(\blacktriangleright\) Следствие: Все три средние линии треугольника делят его на четыре равных треугольника, и, как следствие, равных по площади.
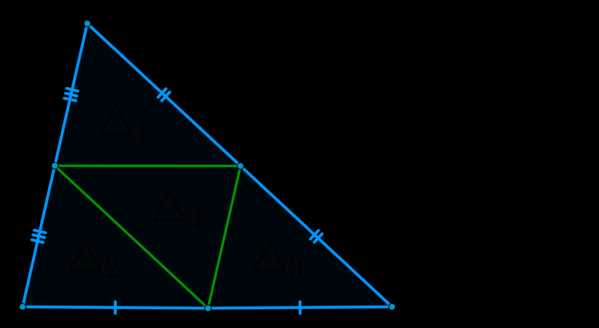
Доказательство: \(\triangle_1, \triangle_2, \triangle_3 \sim \triangle ABC\) с коэффициентом подобия \(\dfrac12\). Следовательно, \(S_{\triangle_1}=S_{\triangle_2}=S_{\triangle_3}=\dfrac14S_{\triangle ABC} \Rightarrow S_{\triangle_4}=S_{\triangle ABC}-3S_{\triangle_1}=\dfrac14S_{\triangle ABC}\)
shkolkovo.net
Вычисление площадей плоских фигур с помощью интеграла
На этом уроке будем учиться вычислять площади плоских фигур, которые ограничены осью абсцисс (Ox), отрезками прямых x = a, x = b и графиком непрерывной и неотрицательной функции y = f(x) для значений «икса», принадлежащих отрезку [a, b]. Такая фигура называется криволинейной трапецией. Боковые отрезки могут вырождаться в точки.
Примеры таких фигур — на рисунке ниже.
Площадь s этой криволинейной трапеции может быть вычислена по формуле
(1).
Итак, определённый интеграл от неотрицательной непрерывной функции f(x) по [a, b] (график функции расположен выше оси Ox) численно равен площади криволинейной трапеции с основанием [a, b], ограниченной сверху графиком функции y = f(x). В этом заключается геометрический смысл определённого интеграла. Рисунки таких фигур — в примерах.
Если же f(x) ≤ 0 (график функции расположен ниже оси Ox), то площадь криволинейной трапеции может быть вычислена по формуле
. (2)
Есть ещё случаи, когда и верхняя, и нижняя границы фигуры — функции, соответственно y = f(x) и y = φ(x), то площадь такой фигуры вычисляется по формуле
. (3)
Таким образом, вычисление площадей плоских фигур — одна из важнейших прикладных задач, в которой определённый интеграл находит наиболее плодотворное применение. Все мы изучали сведения из элементарной геометрии, которые позволяют вычислять площади прямолинейных фигур — прямоугольников, треугольников и многоугольников. Что же касается криволинейных фигур, то здесь для нахождения площади средств из элементарной геометрии уже недостаточно. Итак, к делу. Учимся применять то, что изложено в самом верху этой статьи.
Начнём со случаев, когда площадь фигуры может быть вычислена по формуле (1).
Пример 1. Найти площадь фигуры, ограниченной графиком функции , осью абсцисс (Ox) и прямыми x = 1, x = 3.
Решение. Так как y = 1/x > 0 на отрезке [1; 3], то площадь криволинейной трапеции находим по формуле (1):
.
Пример 3. Найти площадь фигуры, ограниченной графиком функции , осью абсцисс (Ox) и прямой x = 4.
Решение. Фигура, соответствующая условию задачи — криволинейная трапеция, у которой левый отрезок выродился в точку. Пределами интегрирования служат 0 и 4. Поскольку , по формуле (1) находим площадь криволинейной трапеции:
.
Пример 4. Найти площадь фигуры, ограниченной линиями , , и находящейся в 1-й четверти.
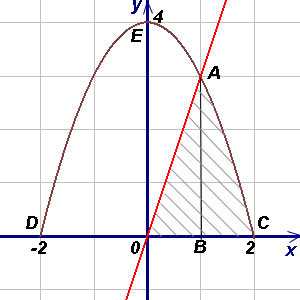
Решение. Чтобы воспользоваться формулой (1), представим площадь фигуры, заданной условиями примера, в виде суммы площадей треугольника OAB и криволинейной трапеции ABC. При вычислении площади треугольника OAB пределами интегрирования служат абсциссы точек O и A, а для фигуры ABC — абсциссы точек A и C (A является точкой пересечения прямой OA и параболы, а C — точкой пересечения параболы с осью Ox). Решая совместно (как систему) уравнения прямой и параболы, получим (абсциссу точки A) и (абсциссу другой точки пересечения прямой и параболы, которая для решения не нужна). Аналогично получим , (абсциссы точек C и D). Теперь у нас еть всё для нахождения площади фигуры. Находим:
Пример 5. Найти площадь криволинейной трапеции ACDB, если уравнение кривой CD и абсциссы A и B соответственно 1 и 2.
Решение. Выразим данное уравнение кривой через игрек: Площадь криволинейной трапеции находим по формуле (1):
.
Переходим к случаям, когда площадь фигуры может быть вычислена по формуле (2).
Пример 7. Найти площадь, заключённую между осью абсцисс (Ox) и двумя соседними волнами синусоиды.
Решение. Площадь данной фигуры можем найти по формуле (2):
.
Найдём отдельно каждое слагаемое:
.
.
Окончательно находим площадь:
.
Пример 8. Найти площадь фигуры, заключённой между параболой и кривой .
Решение. Выразим уравнения линий через игрек:
Площадь по формуле (2) получим как
,
где a и b — абсциссы точек A и B. Найдём их, решая совместно уравнения:
Отсюда
Окончательно находим площадь:
И, наконец, случаи, когда площадь фигуры может быть вычислена по формуле (3). Первый из этих примеров предлагается решить самостоятельно, а затем можно посмотреть правильное решение.
Начало темы «Интеграл»
function-x.ru