22.2. Формулы расхода водослива
Многочисленные
эксперименты показывают, что расход  ,
проходящий через неподтопленные
водосливы, зависит от длины водосливного
фронта (ширины водослива
,
проходящий через неподтопленные
водосливы, зависит от длины водосливного
фронта (ширины водослива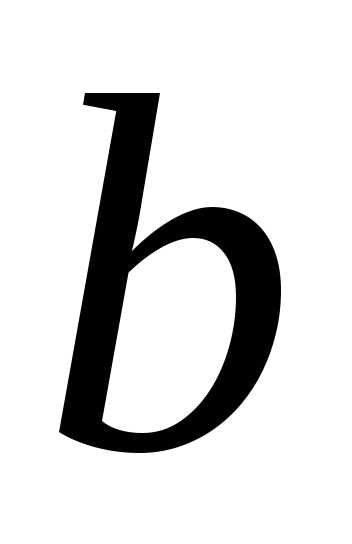 ,
напора над гребнем водослива
,
напора над гребнем водослива ,
скорости подхода
,
скорости подхода ,
ускорения свободного падения
,
ускорения свободного падения ),
т. е.
),
т. е.
,
где — напор с учетом скорости подхода. Для отыскания формулы расхода водослива применим анализ размерностей. Запишем
, (22.1)
где 
Размерность обеих
частей уравнения (22.1) должна быть
одинаковой, так как учтены все факторы,
влияющие на  .
.
Совершенно очевидно
(и это подтверждается данными
экспериментов), что расход  пропорционален ширине водослива
пропорционален ширине водослива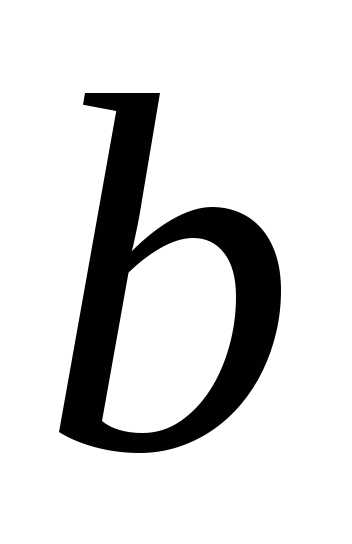 в первой степени. Тогда
в первой степени. Тогда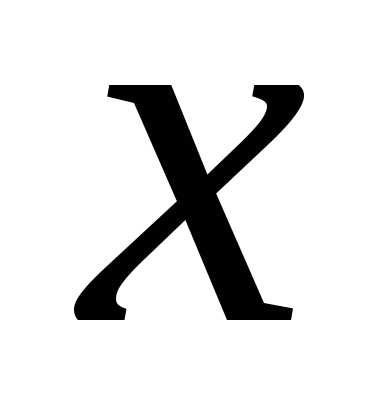 =1.
=1.
Отсюда
.
Приравниваем показатели при и и получаем систему двух уравнений с двумя неизвестными
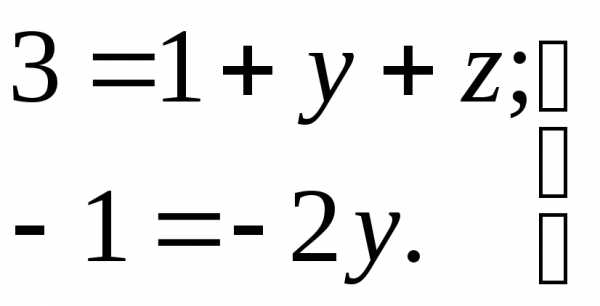
Решая ее, получаем 
 =1,5=3/2.
Тогда
=1,5=3/2.
Тогда.
Обозначив , получим уравнение неподтопленного водослива любого профиля
. (22.2)
Коэффициент 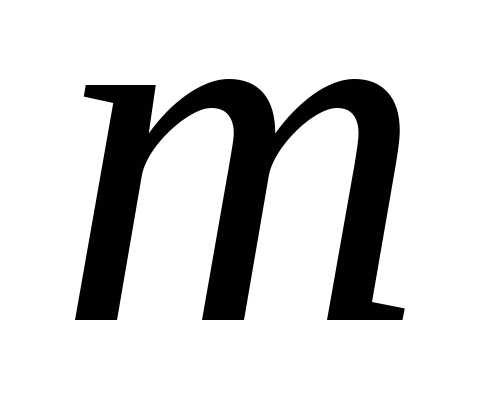 называется коэффициентом расхода
водослива.
называется коэффициентом расхода
водослива.
Часто при расчетах
удобнее учитывать скорость подхода  не в
не в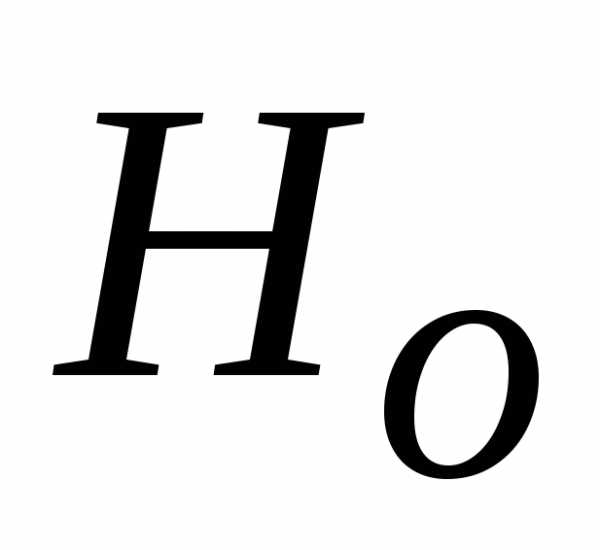 ,
как это сделано в (22.2), а в коэффициенте
расхода. Тогда
,
как это сделано в (22.2), а в коэффициенте
расхода. Тогда
.
Обозначим
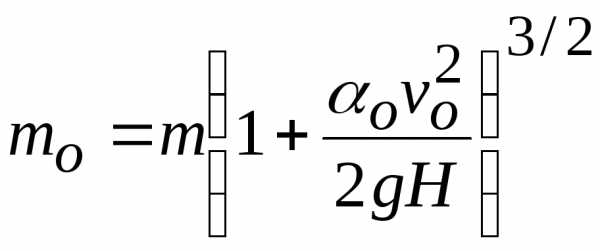 ,
(22.3)
,
(22.3)
отсюда
. (22.4)
Коэффициенты
расхода 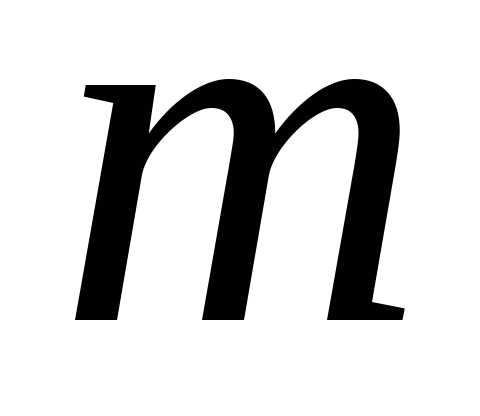 и
и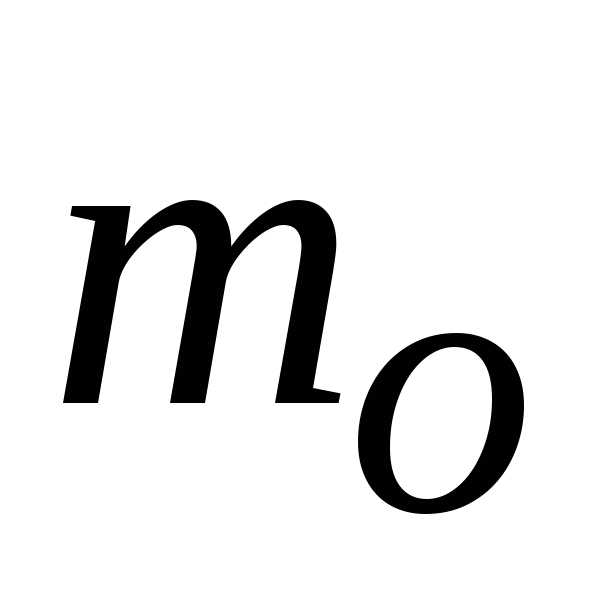 —
безразмерные величины, отражающие
конструктивные особенности водосливов.
—
безразмерные величины, отражающие
конструктивные особенности водосливов.
В формуле (22.4)
скорость подхода учтена в коэффициенте
расхода 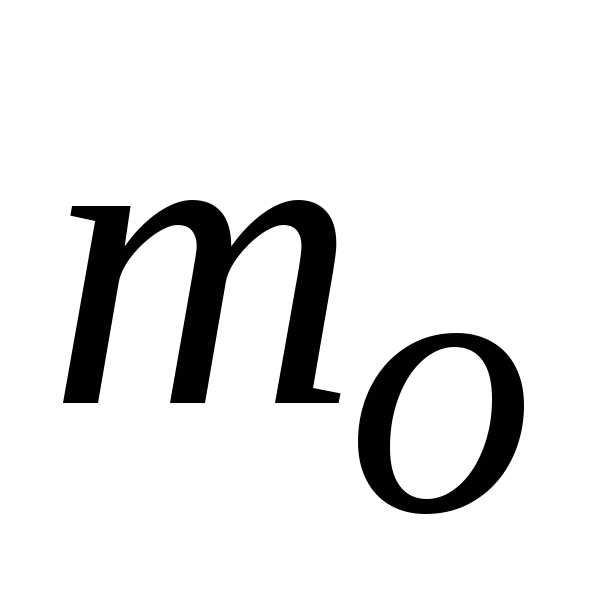 ,
о чем свидетельствует индекс нуль. Из
совместного рассмотрения (22.2) и (22.4)
видно, что
,
о чем свидетельствует индекс нуль. Из
совместного рассмотрения (22.2) и (22.4)
видно, что
. (22.5)
Выразим коэффициент
расхода 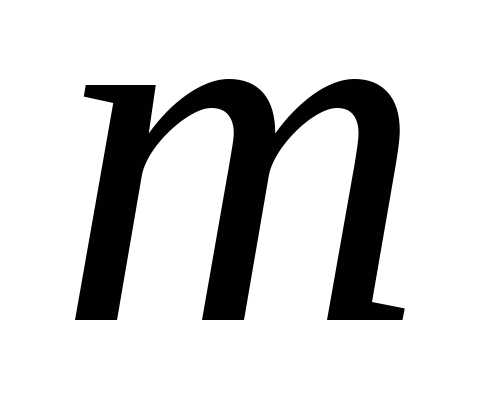 через
через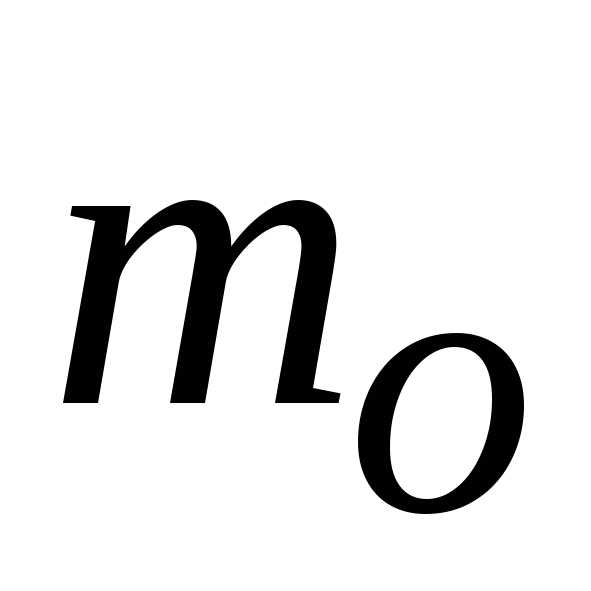 .
Предварительно введем безразмерное
отношение,
где
.
Предварительно введем безразмерное
отношение,
где площадь живого сечения потока в верхнем
бьефе вдали от водослива.
площадь живого сечения потока в верхнем
бьефе вдали от водослива.
Величина 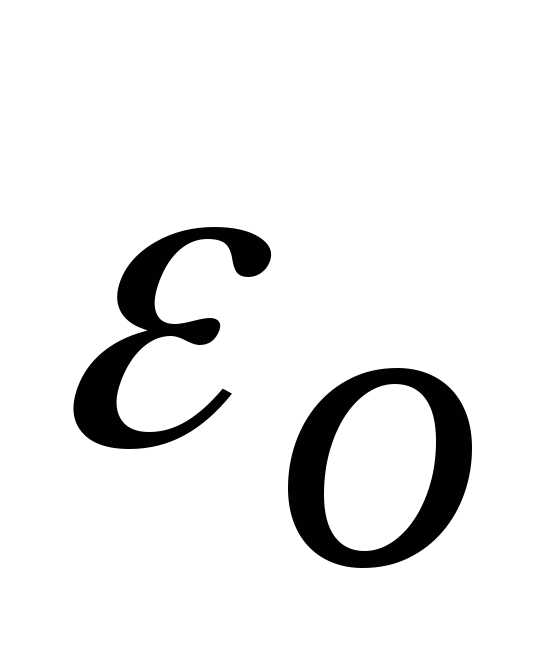 характеризует степень стеснения живого
сечения потока. Тогда
характеризует степень стеснения живого
сечения потока. Тогда
/
Подставив значение расхода из (22.4), найдем, что
.
Далее, обращаясь к (22.5), получим
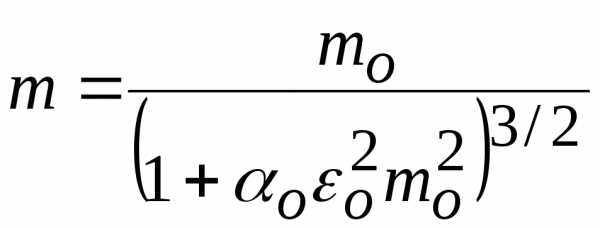 .
(22.6)
.
(22.6)
Для подтопленного
водослива, когда уровень нижнего бьефа
влияет на истечение через водослив, в
формулы (22.2) и (22.4) вводится безразмерный
коэффициент подтопления 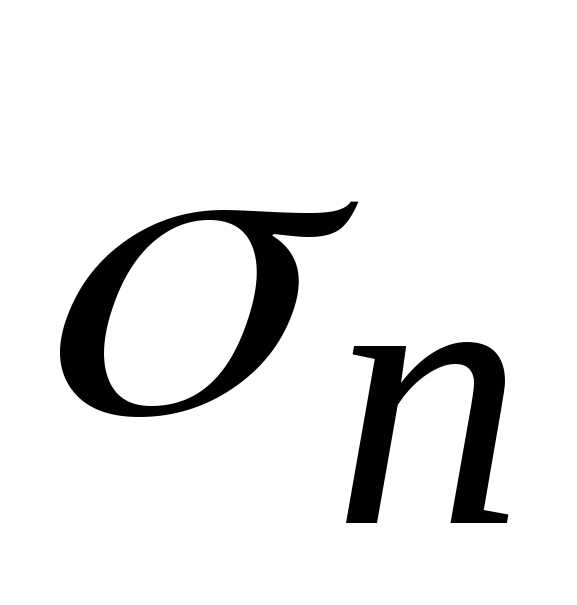 <1.
Тогда расход через подтопленный водослив
определится как
<1.
Тогда расход через подтопленный водослив
определится как
(22.7)
или
. (22.8)
Очевидно, что при
отсутствии подтопления 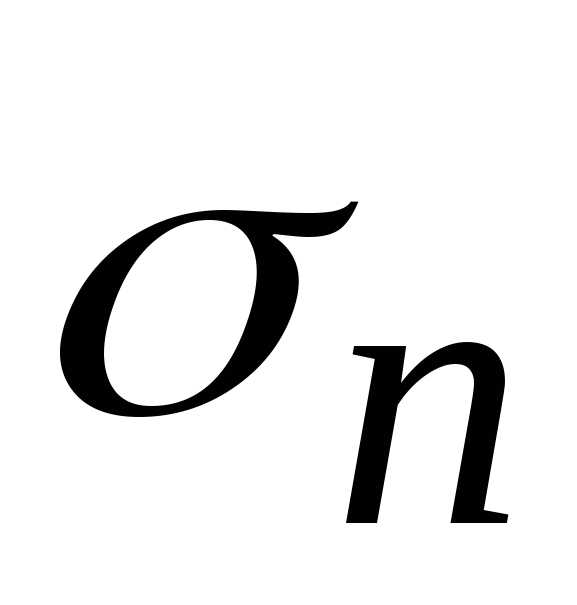 =1
и формулы (22.7) и (22.8) превращаются
соответственно в (22.2) и (22.4).
=1
и формулы (22.7) и (22.8) превращаются
соответственно в (22.2) и (22.4).
22.3. Водосливы с тонкой стенкой (с острым ребром)
Водосливы с тонкой стенкой чаще всего применяются в качестве мерных водосливов, служащих для определения расхода. При истечении через вертикальный прямоугольный неподтопленный водослив с тонкой стенкой без бокового сжатия возможны разные формы струй. В том случае, когда в пространство между струей и стенкой обеспечен доступ воздуха в достаточном количестве и давление вокруг струи равно атмосферному, струя называется свободной (рис. 22.12,а). Водослив с указанными выше признаками называется совершенным (или иногда его называют нормальным).
а) б) в) г)
Рис. 22.12
При отсутствии доступа воздуха под струю возможны следующие формы струи:
поджатая (в сторону водосливной стенки) струя, не подтопленная с нижнего бьефа (рис. 22.12,б). Давление под струей меньше атмосферного, т. е. имеется вакуум и уровень воды поднимается выше уровня в нижнем бьефе, но в подструйном пространстве еще имеется воздуx;
поджатая подтопленная струя (рис. 22.12,в) наблюдается, когда весь воздух унесен потоком и подструйное пространство полностью заполнено водой. Давление под струей (при прочих равных условиях) еще меньше, чем в предыдущем случае;
прилипшая струя (рис. 22.12, г).
Истечение при
отсутствии доступа воздуха, особенно
в первом и последнем случаях, отличается
неустойчивостью. В каждом случае
гидравлический прыжок в нижнем бьефе
(если 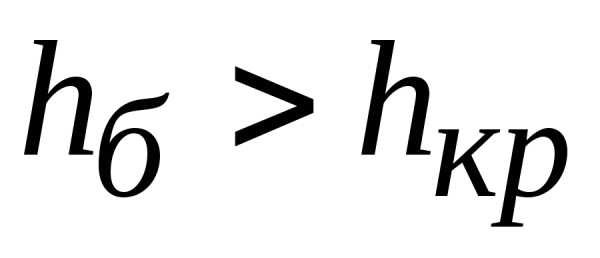 )
может быть как отогнанным, так и
надвинутым.
)
может быть как отогнанным, так и
надвинутым.
Рассмотрим случай истечения через совершенный водослив со свободной струей. Расход, проходящий через соершенный водослив, как и через любой неподтопленный водослив, может быть определен (по 22.4):
.
При известных
коэффициенте расхода 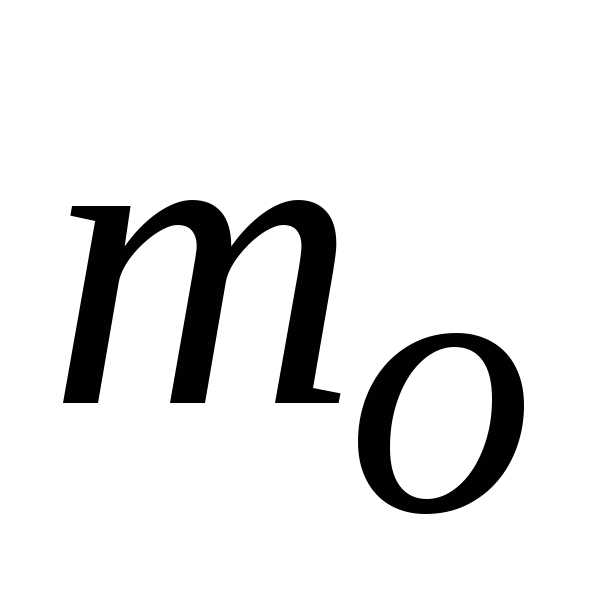 ,
ширине
,
ширине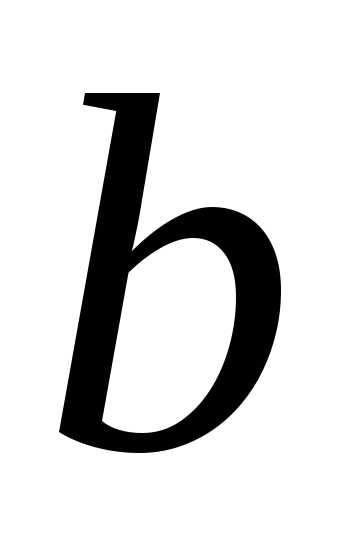 и измеренном напоре
и измеренном напоре однозначно определяем расход
однозначно определяем расход .
.
Коэффициент расхода 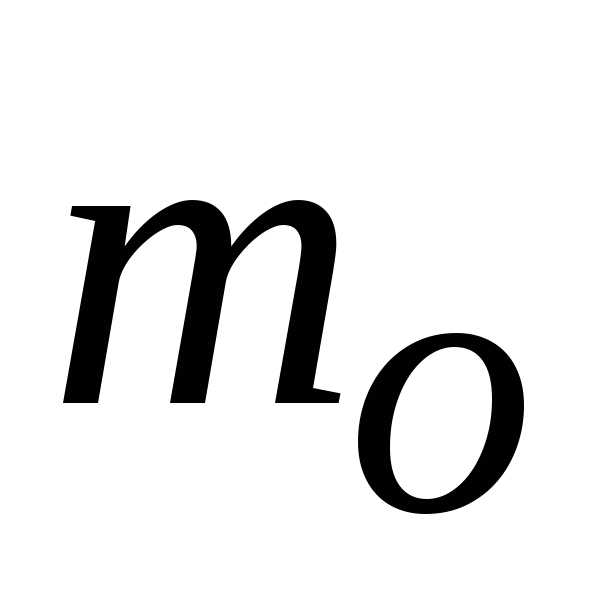 совершенного водослива зависит от
условий подхода потока к водосливу,
которые изменяются с изменением
относительного напора
совершенного водослива зависит от
условий подхода потока к водосливу,
которые изменяются с изменением
относительного напора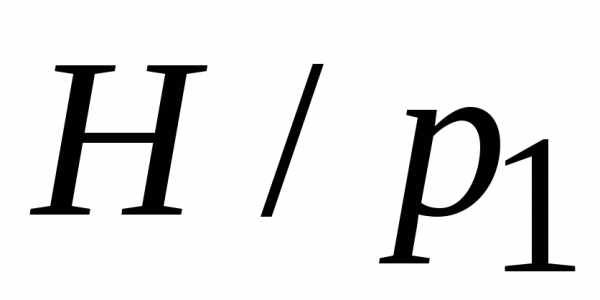 от распределения скорости на подходе,
т. е. в сечении, где измеряется напор, от
поверхностного натяжения жидкости. Для
определения коэффициента могут быть
использованы эмпирические формулы:
от распределения скорости на подходе,
т. е. в сечении, где измеряется напор, от
поверхностного натяжения жидкости. Для
определения коэффициента могут быть
использованы эмпирические формулы:
Базена
(22.9)
или Ребока
.
Члены 0,003/ и 0,0007/
и 0,0007/ учитывают влияние поверхностного
натяжения, значения напора
учитывают влияние поверхностного
натяжения, значения напора в них — в метрах.
в них — в метрах.
Второй сомножитель
(в квадратных скобках) в формуле (22.9)
учитывает влияние скорости подхода  .
.
Для того чтобы
ошибка при определении расхода с помощью
совершенного водослива составляла не
более 1%, необходимо, чтобы 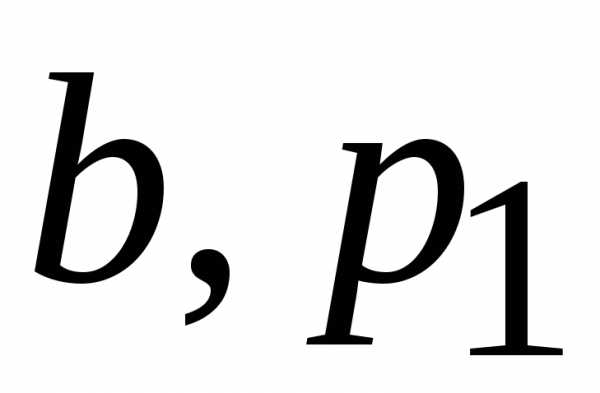 и
и находились в следующих экспериментально
изученных диапазонах: 0,2<
находились в следующих экспериментально
изученных диапазонах: 0,2<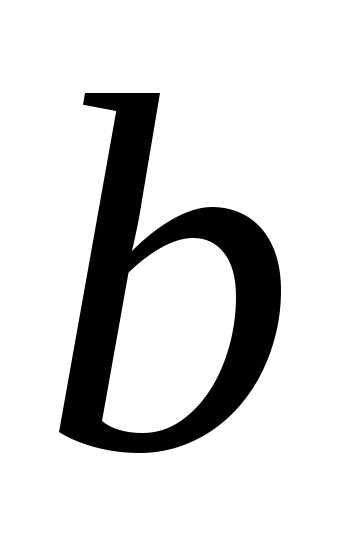 <2м;
0,24<
<2м;
0,24<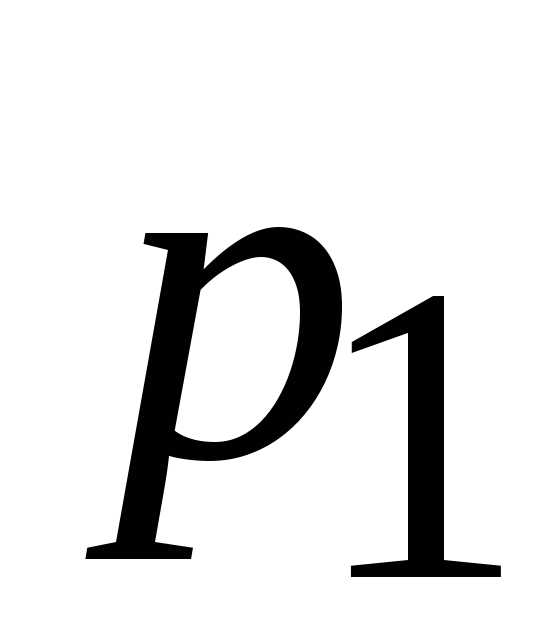
 <1,24м.
При
<1,24м.
При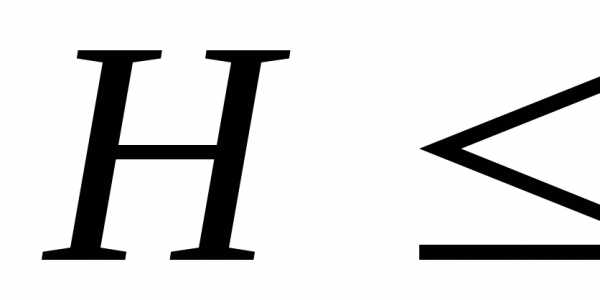 (0,05
(0,05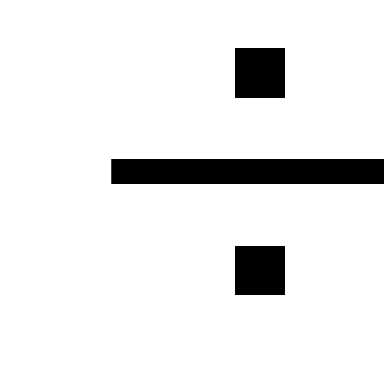 0,07)
м струя становится прилипшей и явление
перестает соответствовать истечению
через совершенный водослив.
0,07)
м струя становится прилипшей и явление
перестает соответствовать истечению
через совершенный водослив. 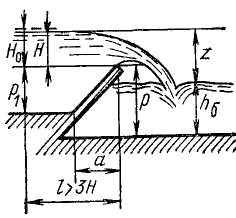
Рис. 22.13
Значение коэффициента
расхода 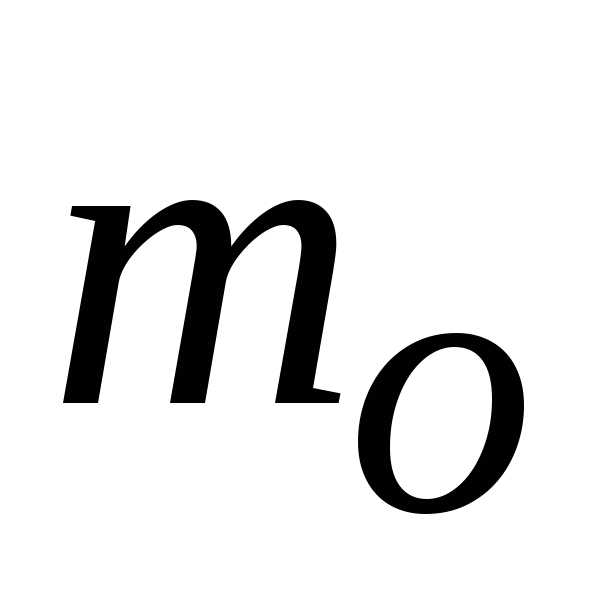 по формуле (22.9) изменяется от 0,409 до 0,49.
по формуле (22.9) изменяется от 0,409 до 0,49.
Для наклонного
неподтопленного водослива без бокового
сжатия (рис. 22.13) со свободной струей
расход определяется по (22.4) с введением
поправочного коэффициента 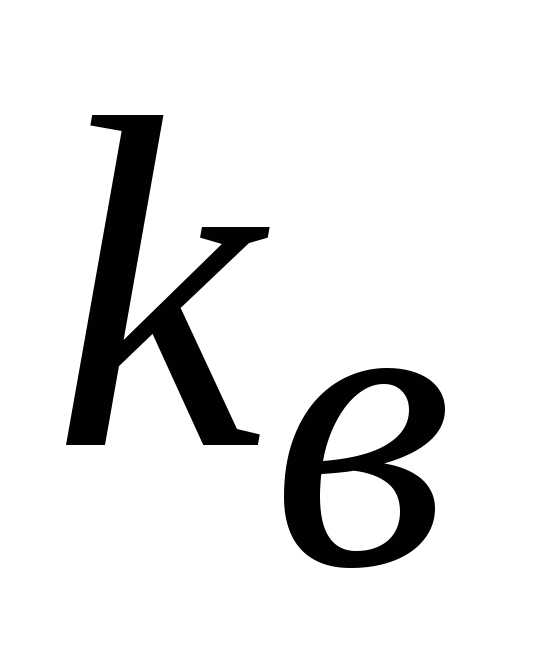 ,
принимаемого по табл. 22.1,
,
принимаемого по табл. 22.1,
Таблица 22.1
Наклон стенки | Поправочный
коэффициент | ||||||||
0 | 1/3 | 2/3 | 1 | 2/1 | 4/1 | 5/1 | 7/1 | 8/1 | |
В сторону верхнего бьефа | 1 1 | 1,05 0,96 | 1,09 0,93 | 1,11 0,91 | 1,13 — | 1,10 — | 1,09 — | 1,07 — | 1,06 — |
studfiles.net
6.3. Определение расходов воды по водосливам
Водосливом называют установленную на пути движения водного потока преграду, через которую переливается вода. Преграда может быть сплошной или с вырезом в ней разной формы. Водосливы широко применяют в качестве подпорных плотинных устройств гидрометрических сооружений для определения расходов воды, шлюзов-регуляторов, водосбросных сооружений при плотинах и пр. Основные элементы водосливов приведены на рис. 19. Участок водосливного сооружения, где происходит перелив воды, называется порогом водослива. Превышение уровня воды перед водосливом (в верхнем бьефе УВБ) над порогом водослива образует напор Н (рис. 19,а). Напор измеряется на свае, установленной на расстоянии трех-пяти величин Н от порога. Величина с (рис. 19,а) характеризует толщину порога водослива.
В зависимости от формы водосливного отверстия водосливы подразделяются на прямоугольные (рис. 19,б), трапецеидальные (рис. 19,в) и треугольные (рис. 19,г). Разделяют водосливы и по толщине порога (толщине стенки). Если толщина порога составляет не более 0,5Н, то такие водосливы относят к водосливам с тонкой стенкой. Водосливы с тонкими стенками можно при небольших расходах воды использовать в качестве водомерных сооружений. Если величина напора более 2Н, то это водослив с широким порогом. Водосливы с широким порогом используются в качестве водосбросных сооружений при плотинах. На пропускную способность водослива влияет уровень воды ниже водослива (в нижнем бьефе). У незатопленных водосливов уровень нижнего бьефа ниже порога водослива и не влияет на расход вод через водослив. У затопленных уровень нижнего бьефа, располагающегося выше порога водослива, снижает расход.
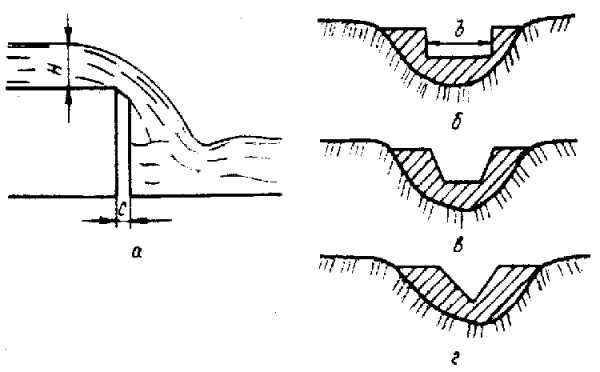
Рис. 19. Водосливы:
а — общий вид; б — прямоугольный; в — трапецеидальный; г — треугольный
Расход воды через водослив определяют по формуле
Q = obH 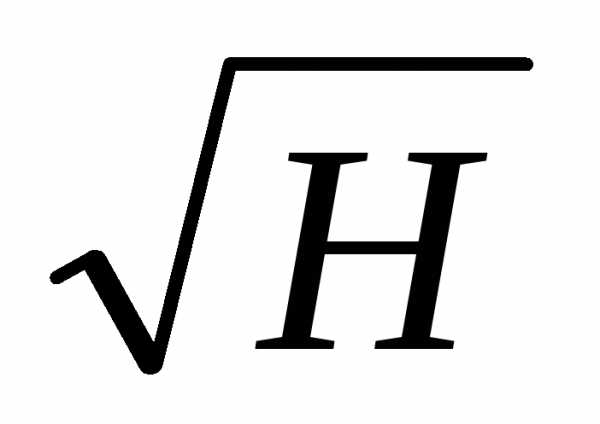 ,
,
где Q — расход, м3/с; b — ширина порога, м; Н — величина напора, м; o — модуль расхода, для незатопленных водосливов o = 1,95.
Расход воды через прямоугольный водослив с широким порогом определяют по формуле
Q = 1,4bH 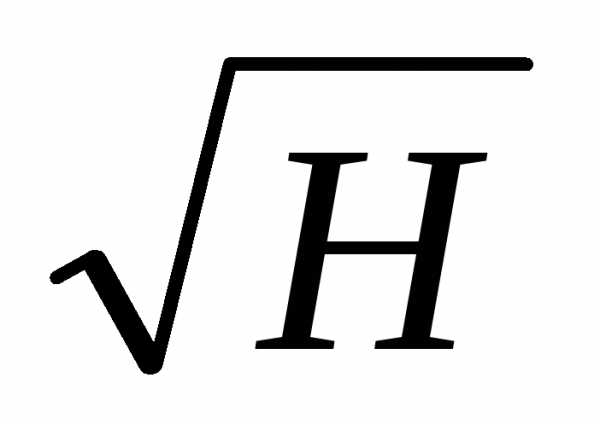 .
.
Расход через водосливы с тонкой стенкой прямоугольного трапецеидального и треугольного сечений (с углом выреза 90°) определяют по формулам:
Qпрямоуг. = 1,95bH 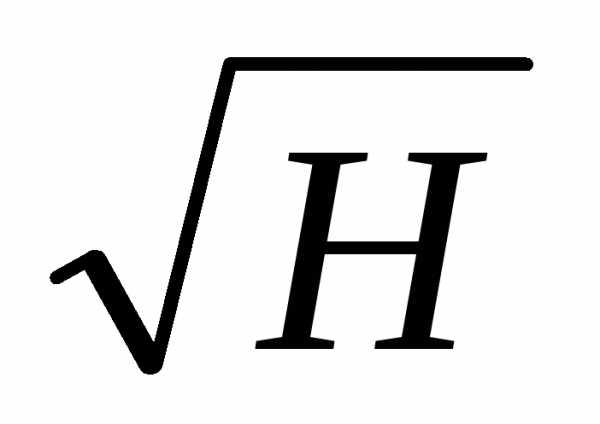 ; Qтрапец. = 1,86bH
; Qтрапец. = 1,86bH 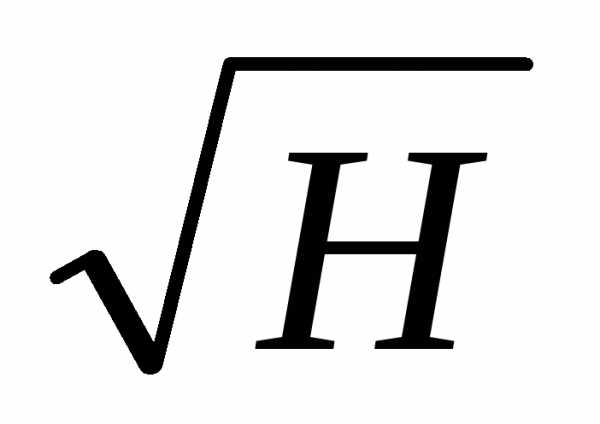 ; Qтреуг. = 1,4H2
; Qтреуг. = 1,4H2 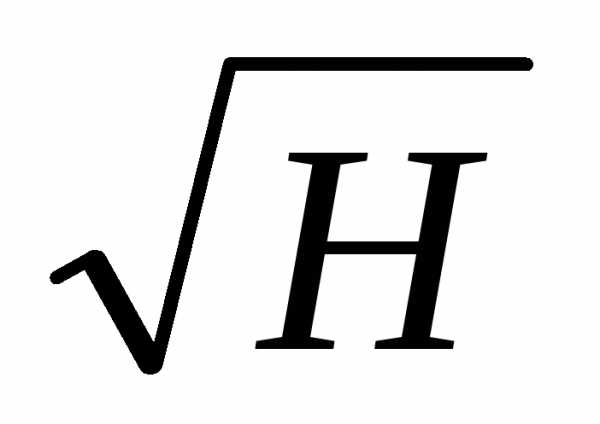 .
.
Водосливы с широким порогом используются в качестве водосбросных сооружений при плотинах. Расход воды через подобные водосливы рассчитывается по формуле
Q = mb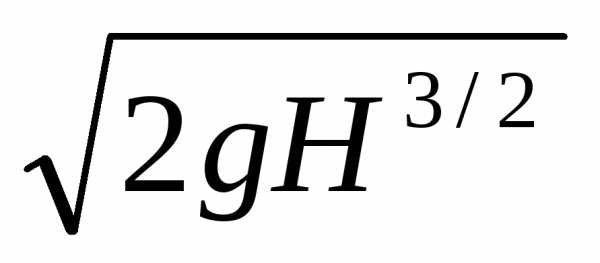 ,
,
где m – коэффициент расхода; b – ширина порога водослива, H – напор, м, g – ускорение силы тяжести (9,81 м/с2).
21
studfiles.net
8.5. Водосливы с тонкой стенкой (с острым ребром)
Водосливы с тонкой стенкой часто применяются в качестве мерных водосливов для определения расхода. Чаще всего истечение через неподтопленный водослив с тонкой стенкой происходит в форме свободной струи, которая образуется в условиях, когда в пространстве под ней атмосферное давление, рис. 8.9. Такая струя является устойчивой.
В случае истечения через затопленный водослив с тонкой стенкой образуется волнистая струя, рис. 8.10.
В случае истечения через водослив со свободной струей расход может быть определен по формуле
(8.2) |
Коэффициент расхода может быть определен по эмпирической формуле
(8.3) |
значения H и P1 измеряются в метрах.
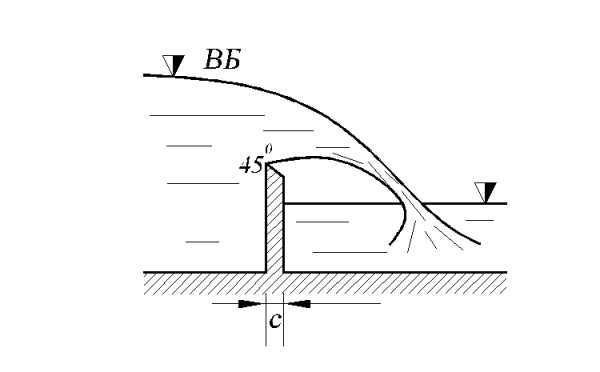
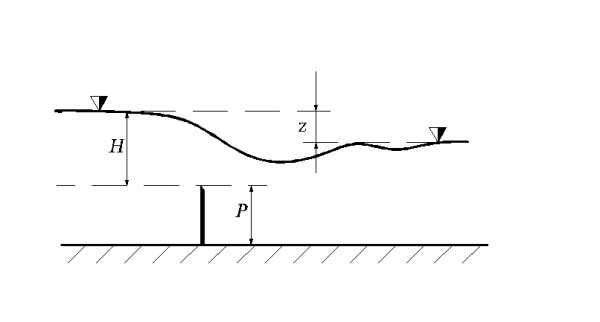
Рис 8.9 Рис. 8.10
8.6. Основные задачи гидравлического расчета водосливов
При расчете водосливов любого типа обычно решается одна из трех задач, что непосредственно следует из основной формулы (8.1), которая содержит три переменные величины Q, b и H.
Задача 1. Найти расход данного водослива Q.
Задача 2. Найти ширину водослива b.
Задача 3. Найти напор на водосливе H.
Все эти три задачи решаются простым вычислением, если известны значения коэффициента расхода m.
8.7.Водослив с широким порогом
Течение на водосливе с широким порогом устанавливается почти с неизменной глубиной h<H, поэтому, возникают два перепада: Z– разность отметок свободной поверхности верхнего и нижнего бьефов и Z´ — разность отметок свободной поверхности верхнего бьефа и свободной поверхности на пороге водослива, рис. 8.11.
В данном случае необходимо решить две основные задачи: определение глубины воды h на пороге и определение коэффициента расхода m.
Известно решение для глубины на водосливе, в основе которого предположение о минимуме энергии, т.е. на водосливе с широким порогом должна устанавливаться глубина h = hкр, при которой удельная энергия сечения достигает минимального значения, а глубина равна
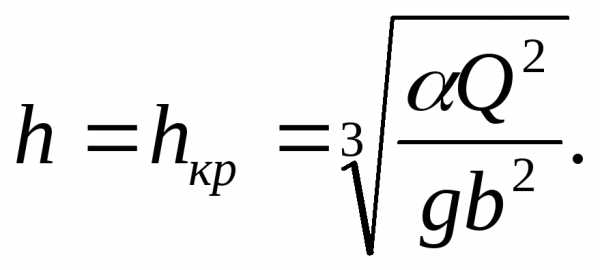
Установим связь критической глубины hкр с напором H0. Из уравнения Бернулли для двух сечений I и II, рис. 8.11 получим
(8.4) |
С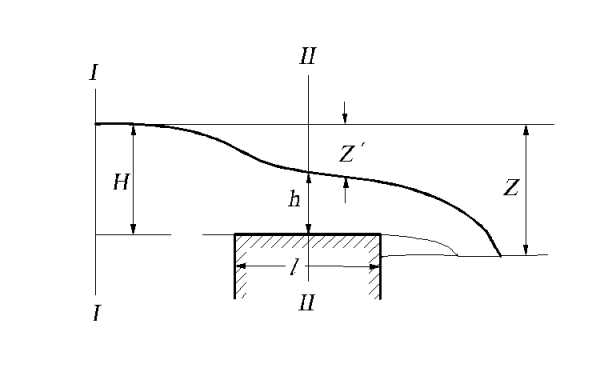 учетом того, чтои известного соотношения
учетом того, чтои известного соотношения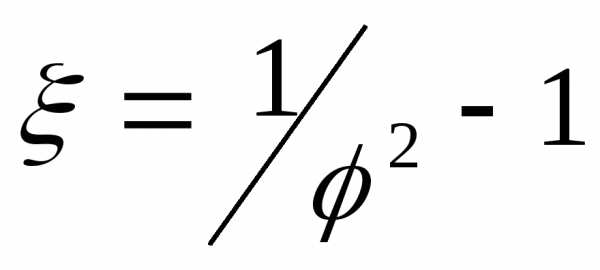 уравнение (8.4) можно переписать так
уравнение (8.4) можно переписать так
Рис. 8.11
Обозначая
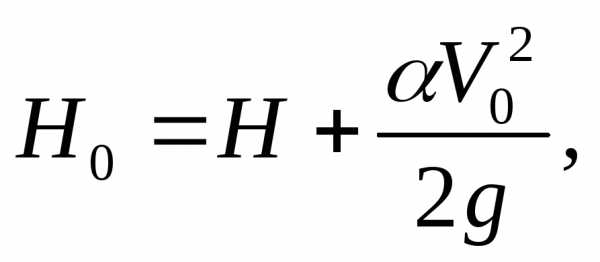 получим
получим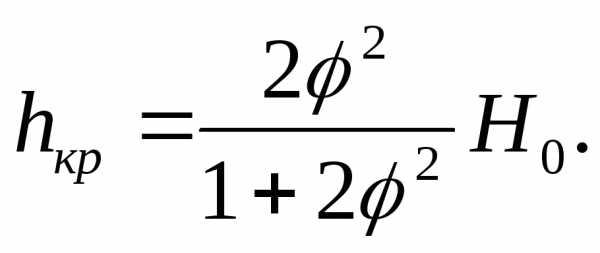
Введем обозначение
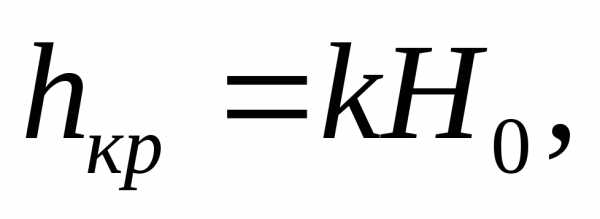 где
где 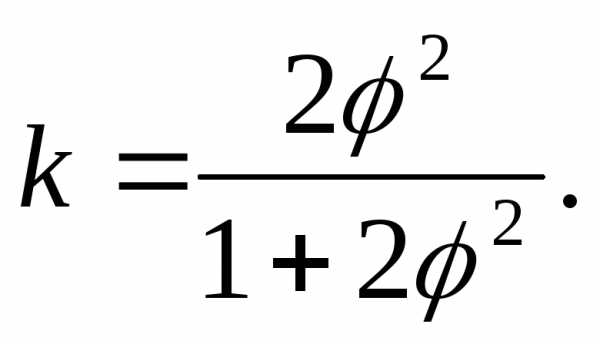
Запишем уравнение расхода через водослив
или
Сопоставляя эту формулу с общей формулой расхода через водослив
получим
Если 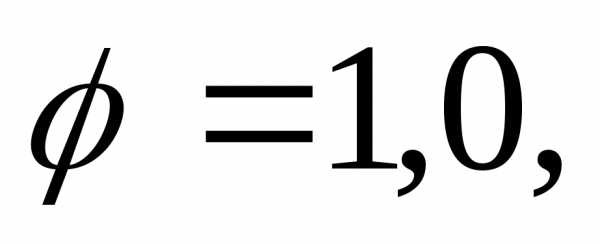 тоm = 0,385, что является наибольшим значением
для коэффициента расхода водослива с
широким порогом. Обычно m = 0,32 – 0,35.
тоm = 0,385, что является наибольшим значением
для коэффициента расхода водослива с
широким порогом. Обычно m = 0,32 – 0,35.
8.8.Затопленный водослив с широким порогом
Опыты показали, что затопление водослива начинается лишь при условии
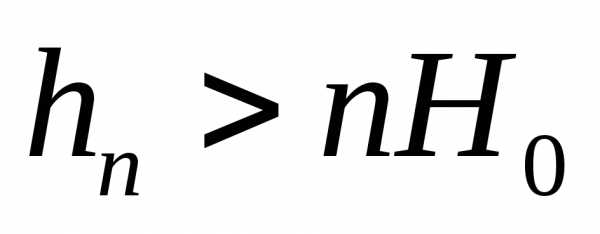 ,
,
где коэффициент n достигает значения 0,8 и более. Глубина 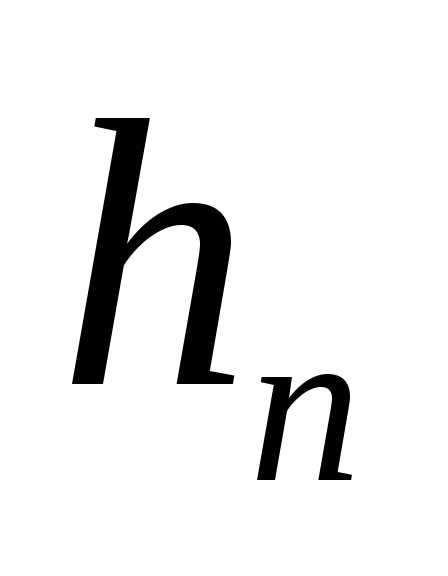 представляет собой расстояние от
свободной поверхности в нижнем бьефе
до порога водослива.
представляет собой расстояние от
свободной поверхности в нижнем бьефе
до порога водослива.
Предложена зависимость для определения критического значения глубины затопления hn
.
Если , то водослив затоплен.
Скорость течения и расход в этом случае определяются по следующим формулам
,
.
Задача 8.1 Определить расход через прямоугольный водослив с тонкой стенкой без бокового сжатия и со свободным доступом воздуха под струю. Дано: ширина водослива b =0,8 м;p1 = 0,5 м; H = 30см.
Решение. Коэффициент расхода по формуле (8.3) равен
.
Расход без поправки на скорость подхода по формуле (8.1)
Найдем поправку на скорость подхода
.
Тогда по формуле:
откуда окончательно:
studfiles.net
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ РАСХОДА И СКОРОСТИ, ПОСТРОЕНИЕ СВОБОДНОЙ ПОВЕРХНОСТИ НА ВОДОСЛИВЕ С ШИРОКИМ ПОРОГОМ
1. ЦЕЛЬ РАБОТЫ
Определить коэффициенты расхода и скорости неподтопленного водослива с широким порогом и коэффициенты расхода, подтопления и скорости подтопленного водослива с широким порогом.
Построить кривые свободной поверхности для неподтопленного и подтопленного водослива с широким порогом.
2. ОБЩИЕ СВЕДЕНИЯ
Водосливом с широким порогом называют водослив с горизонтальной поверхностью порога при 2 < < 10, где S — ширина (толщина) порога водослива. При такой ширине порога потери напора по длине малы и не учитываются при расчете водосливов. В зависимости от относительной ширины на пороге водослива устанавливаются различные формы свободной поверхности (рисунки 5.1 и 5.2).
Несмотря на сложную форму движения воды на пороге, можно выделить ряд сечений, в которых кривизна свободной поверхности мала или может считаться равной нулю. В этих сечениях давления распределяются по гидростатическому закону и устанавливается глубина h на пороге водослива, которая является расчетной при выводе формулы, истечения через водослив с широким порогом. Формула, по которой определяется расход водослива, имеет вид:
(5.1)
где ϕ — коэффициент скорости;
b — ширина водосливного фронта, м;
h — глубина воды на пороге водослива, м;
Н0 — напор с учетом скорости подхода, м.
Выражение (5.1) после преобразования приводится к общей формуле водослива:
(5.2)
где m — безразмерный коэффициент расхода водослива.
Напор с учетом скорости подхода определяется из выражения
(5.3)
где -скорость подхода к водосливу, м/с;
α — коэффициент Кориолиса (α ≈ 1,1).
Значения коэффициентов m иϕ
Эксперименты показывают, что при движении потока через водослив решающее влияние на коэффициент m оказывают сопротивления, отражаемые коэффициентом скорости ϕ. Сопротивления для неподтопленного водослива зависят от относительной высоты порога , формы порога на входе, бокового сжатия, формы входа в плане и относительного напора . В таблице 5.1 приводится зависимость коэффициента расхода m от коэффициента скорости ϕ, а в таблице 5.2 — зависимость коэффициента расхода для водослива с широким порогом без бокового сжатия от
Таблица 5.1
| ϕ | 0,94 | 0,96 | 0,97 | 0,98 | 1,0 |
| m | 0,3 | 0,32 | 0,34 | 0,36 | 0,385 |
Таблица 5.2
| 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | 2,0 | 4,0 | 6,0 | |||
| m | 0,385 | 0,366 | 0,356 | 0,350 | 0,45 | 0,342 | 0,333 | 0,327 | 0,325 | 0,320 |
Подтопленный водослив с широким порогом
Подтопление водослива с широким порогом наступает лишь после того, как уровень воды в нижнем бьефе поднимется над порогом выше определенного предела. Этот предел, при котором наступает подтопление водослива зависит от величины (Δ — превышение уровня воды в нижнем бьефе над порогом водослива, Δ = h6 — Р).
На рисунке 5.2 представлена схема подтопленного водослива. На пороге водослива устанавливается спокойное состояние потока с глубинами большими критической глубины hкр.
Подтопление водослива наступает при следующих значениях :
— при плавном входе на порог
(5.4)
— при неплавном входе на порог
(5.5)
Значения коэффициентов расхода m и скорости ϕ для подтопленного водослива с широким порогом по данным Д.И. Кумина приводятся в таблице 5.3.
Таблица 5.3
| ϕn | 0,76 | 0,84 | 0,90 | 0,96 | 0,99 | |
| m | 0,30 | 0,32 | 0,34 | 0,36 | 0,38 | 0,385 |
Расчетная формула для подтопленного водослива с широким порогом без учета перепада восстановления имеет вид:
(5.6)
где — коэффициент скорости подтопленного водослива.
Выражение (5.6) после преобразования приводится к общей формуле водослива:
(5.7)
где — безразмерный коэффициент подтопления.
а)
б)
в)
г)
Рисунок 5.1 — Неподтопленный водослив с широким порогом
Рисунок 5.2 — Подтопленный водослив с широким порогом
3. ОПИСАНИЕ ОПЫТНОЙ УСТАНОВКИ
На рисунке 1.1 представлена схема опытной установки. Вода по трубопроводу 1 подается в приемную камеру 3. Расход воды регулируется с помощью задвижки 2. Напор воды на водосливе-водомере 5 измеряется с помощью пьезометра 4. В средней части лотка 6 устанавливается исследуемый водослив с широким порогом шириной S =0,32 м. В паз 7 вставлен затвор, который используется для изменения режима движения жидкости в лотке и на пороге водослива.
4. ПОРЯДОК ПРОВЕДЕНИЯ РАБОТЫ
Для установившегося движения на водосливе с широким пороем (для одной из схем, представленных на рисунках 5.1 и 5.2) определяют отметки уровня воды, порога водослива и дна лотка. Данные заносят в таблицу 5.4. Расстояния между створами и количество створов даны на рисунке 5.3.
Расход воды определяется по тарировочной кривой при помощи водослива-водомера.
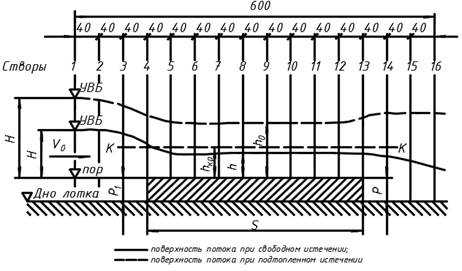
Рисунок 5.3 — Схема к построению кривой свободной поверхности на водосливе с широким порогом
5. ПОРЯДОК РАСЧЕТА
Расчет производится в табличной форме (таблица 5.5)
1. Определяется высота водослива
2. Находится напор в сечении 1-1 (рисунок 5.3)
3. Вычисляется скорость подхода из выражения
где — площадь живого сечения потока перед водосливом, м2;
— расход по тарировочной кривой, м3/с.
4. Определяется напор с учетом скорости подхода по формуле (5.3).
5. Находится глубина на пороге водослива в сечении 9-9, где давления распределяются по закону близкому к гидростатическому
6. Вычисляются опытные значения коэффициентов расхода т, коэффициентов скорости ϕ и ϕn коэффициента подтопления σn из формул (5.1), (5.2), (5.6), (5.7):
где — глубина в сечении 9-9 для неподтопленного водослива, м;
где — коэффициент расхода подтопленного водослива;
— полный напор подтопленного водослива, м;
— глубина в сечении 9-9 для подтопленного водослива, м.
7. Опытные коэффициенты m, ϕ, ϕn сравниваются со справочными их значениями (таблицы 5.1, 5.2 и 5.3) и делается вывод.
| Наименование | Сечения | ||||||||||||||||||||||||||||
| 1. Расстояние между сечениями, м | 1-2 | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | 8-9 | 9-10 | 10-11 | 11-12 | 12-13 | 13-14 | 14-15 | |||||||||||||||
| 2. Отметки поверхности струи, м | |||||||||||||||||||||||||||||
| 3. Отметка порога, м | |||||||||||||||||||||||||||||
| 4. Глубина на пороге, м | |||||||||||||||||||||||||||||
| 5. Критическая глубина, hкр, м | |||||||||||||||||||||||||||||
Таблица 5.4 — Данные для построения профиля струи
Таблица 5.5 — Опытные данные
| Наименование | Водослив | |
| неподтопленный | подтопленный | |
| 1. Отметка дна лотка 𝛁дна, м | ||
| 2. Отметка порога водослива, м | ||
| 3. Высота порога водослива, м | ||
| 4. Отметка уровня воды перед водосливом (сечение 1-1), м | ||
| 5. Напор воды над порогом водослива Н, м | ||
| 6. Ширина водослива b, м | ||
| 7. Расход воды Q*10-3, м3/с (по тарировочной кривой) | ||
| 8. Скорость подхода Vo, м/с | ||
| 9. Скоростной напор , м | ||
| 10. Полный напор Но, м | ||
| 11. Отметка поверхности воды на пороге (сечение 9-9), м | ||
| 12. Глубина на пороге h, м | ||
| 13. Коэффициент расхода т | ||
| 14. Коэффициент скорости ϕ | ||
| 15. Коэффициент подтопления |
ЛАБОРАТОРНАЯ РАБОТА №6
cyberpedia.su
17.5. Водослив практического профиля
В гидротехнической практике чаще других встречаются водосливы практического профиля или с широким порогом. Водосливные плотины гидроэлектростанций, головных сооружений оросительных систем и т.д. представляют собой водосливы практического профиля. Водосливы практического профиля могут иметь различные очертания: криволинейного (рис. 17.7), прямоугольного (рис. 17.8), полигонального профиля (рис. 17.9). В гидротехнической практике наибольшее применение получили водосливы криволинейных форм.
Рис. 17.8 Рис. 17.9
Незатопленный водослив. Водослив практического профиля считается незатопленным, если уровень нижнего бьефа лежит ниже гребня водослива (рис. 17.10).
hb< p.
Формула расхода через незатопленный водослив практического профиля имеет вид общей формулы водосливов (17.1). Но так как на практике подводящее русло у водосливных плотин обычно имеет неправильное сечение, в формуле расхода водослива практического профиля необходимо учитывать скорость подхода и боковое сжатие потока. Влияние скорости подхода V0 учитывается путем исправления напора Н на величину скоростного напора скорости подхода
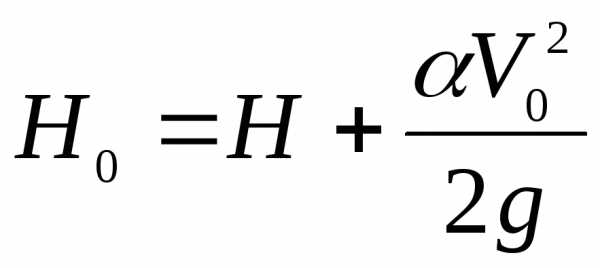 .
.
Влияние бокового сжатия потока учитывается введением поправочного коэффициента на сжатие струи (при ориентировочных расчетах значение коэффициента бокового сжатия принимается в пределах ε = 0,86 – 0,95 или в среднем ε ≈ 0,90). Расчетная формула расхода через незатопленный водослив практического профиля имеет вид
. (17.3)
Коэффициент расхода m для водосливов практического профиля изменяется в широких пределах в зависимости от формы стенки водослива, величины напора и т.д. В качестве средних значений для коэффициента расхода можно принимать следующие:
Для водосливов криволинейного профиля
m = 0,45 – 0,49.
2. Для водосливов прямоугольного и полигонального профиля
m = 0,40 – 0,43.
17.6. Водослив с широким порогом
Водосливом с широким порогом называется водослив, имеющий горизонтальный порог, длина которого δ в 2-3 раза превышает напор Н (рис. 17.11). Обычно считается, что на пороге его имеет место плавноизменяющееся движение, близкое к параллельно-струйному.
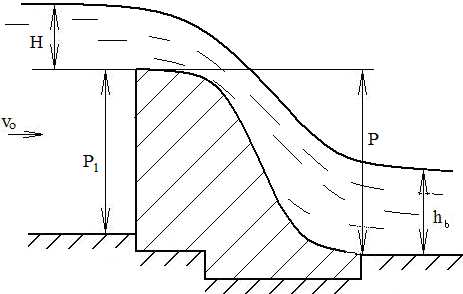
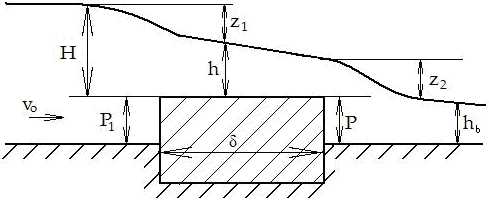
Рис. 17.10 Рис. 17.11
Незатопленный водослив. Незатопленный водослив с широким порогом характеризуется наличием двух перепадов свободной поверхности – в начале и в конце порога (рис. 17.11). Водослив считается незатопленным, когда уровень нижнего бьефа расположен ниже порога водослива, или когда высота подтопления меньше 0,8 напора, т.е. условие незатопленного водослива с широким порогом будет
hb< p или (hb— p) < 0,8 Н.
В конце горизонтальной части порога устанавливается примерно постоянная глубина h = hк – критическая глубина.
Расход через незатопленный водослив с широким порогом определяется по формуле (17.3). Коэффициент расхода водослива с широким порогом при отсутствии бокового сжатия изменяется в пределах m = 0,320-0,385 и может быть определен по специальным формулам.
Затопленный водослив. Водослив с широким порогом считается затопленным, когда уровень нижнего бьефа находится выше порога водослива на величину более 0,8 Н0. Все необходимые коэффициенты для расчета водосливов с широким порогом берутся из таблиц или по полуэмпирическим формулам и здесь не приводятся.
studfiles.net
Водослив расход — Справочник химика 21
Водослив с острой кромкой. Расход жидкости через такой водослив можно определить по аналогии с определением расхода жидкости через затопленное отверстие по формуле [c.59]Различают водосливы с боковым сжатием, если ширина водослива Ь меньше ширины канала В (рис. 6-20, а), и без бокового сжатия, если Ь = В. Водосливы называют незатопленными, если Н >к (рис. 6-20, а), и затопленными, если Н уровень жидкости за водосливом, Н — высота порога. Расход жидкости через прямоугольный водослив без бокового сжатия определяется из формулы [c.168]
Тогда расход жидкости через водослив составит [c.168]
Так как через водослив при подпоре Лг должно стекать 85% общего расхода воды, то фактический расход ее через водослив составляет [c.137]
Общей формулой для подсчета расхода, перетекающего через водослив, является [c.110]
Пример 4.5. В конденсаторе смешения требуется установить горизонтальные полки-перегородки (рис. 4.14). Расход воды Р =30 м ч. Диаметр корпуса конденсатора Д=1,4 м. Высота планки для слива воды Ло=20 мм. Сколько отверстий диаметром й=2 мм необходимо проделать в полках, чтобы, через эти отверстия стекало 15% расходуемой воды, а через водослив — 85% [c.137]
Для распределительных желобов рекомендуются следуюпще размеры ширина не менее 120 мм высота не более 350 мм скорость жидкости в желобе не более 0,3 м/с. Расстояние от прорези до дна желоба и до торцевой стенки должно быть больше ширины прорези не менее чем в 3 раза. Высота прямоугольной прорези принимается несколько большей высоты подпора жидкости, определяемой из уравнения расхода жидкости через водослив [c.228]
Расход жидкости через водослив определяется по общей формуле истечения [c.51]
Если водослив имеет форму круга или прямоугольника, то при истечении через него жидкости возникает боковое сжатие и коэффициент расхода будет несколько меньше. Практически в этом случае можно принять 1о=0,4 и расход жидкости определить, по формуле [c.51]
Прошедшая приемную камеру сточная вода через треугольный водослив сливается в регулирующий резервуар 1, объем которого зависит от суточного расхода и коэффициента неравномерности поступления стока. Из резервуара вода насосом через дозирующий бачок с переливным устройством в расчетном количестве направляется в анаэробный реактор первой ступени 2, а избыточная часть воды возвращается в регулирующий резервуар. [c.164]
Пропорциональный водослив (рисунок 93) применяется для измерения расхода сточных вод, содержащих взвеси в прямоугольных лотках и каналах, когда перепад уровней обеспечивает работу водослива в незатопленном режиме. [c.272]
Знаком отмечены случаи, когда максимальный расход должен быть не более 85% верхнего предела измерений, указанного в данной графе. Например, водослив Л-30-60-111. можно применить с уровнемером Ьп=630 мм лля измерения расхода О а =500 0,85=425 м7ч. [c.274]
Распределительные желоба принимаются следующих размеров ширина не менее 120 мм, высота не более 350 мм, при этом скорость движения жидкости в желобе не должна превышать 0,3 м/с. Высота прямоугольной прорези принимается больше высоты подпора жидкости, определяемой из уравнения расхода жидкости через водослив [c.100]
Пропорциональный водослив (вариант П) (рис. 5.41). Пропорциональный водослив применяется для измерения расхода сточных вод и других жидкостей, содержащих взвеси в прямоугольных лотках и каналах, когда перепад уровней обеспечивает работу водослива в незатопленном режиме. [c.160]
Водослив с порогом треугольного профиля (вариант 111) (рис. 5.42). Измерительный водослив с порогом треугольного профиля применяется для измерения расхода бытовых и производственных сточных вод до 20 000 м /ч в относительно широких каналах (й/В 0,5) [3]. [c.162]
Увеличение диаметра, вынос иловых приямков в середину зоны отстаивания, усовершенствованный водослив, предварительная аэрация позволяют повысить пропускную способность отстойников и значительно сократить капитальные расходы и эксплуатационные затраты на их сооружение. [c.78]
В некоторых химических аппаратах на пути потока жидкости устанавливают тонкий перегораживающий порог, через который происходит перелив жидкости струей плоского сечения толщиною Л (рис. 1-15, г). Такое устройство называется водосливом. Вдали от порога уровень жидкости над ним // > Л, поэтому скорость подхода жидкости к порогу намного меньше скорости переливающейся струи и может практически не учитываться. В таком случае расход жидкости через водослив можно рассматривать как истечение через отверстие (без верхней стороны) высотой к и шириною, рав юй ширине порога Ь [c.67]
Расход жидкости через прямоугольный водослив [c.97]
Различают незатопленные и затопленные водосливы. Для первых из них характерно то, что течение через водослив не зависит от состояния жидкости за водосливом, для вторых такая зависимость имеет место. Расход жидкости через водослив рассчитывается так же, как при истечении из большого отверстия — уравнение (111.53). Обычно высоту уровня жидкости отсчитывают от [c.212]
Затопление водослива наступает при условии, что высота уровня жидкости за ним превышает высоту перегородки h и отношение h к разности уровней до и после перегородки 2 больше 1,4 (рис. III. 8). Это отношение возрастает с уменьшением расхода жидкости через водослив. С увеличением расхода жидкости z возрастает, и при hjz возникает явление так называемого гидравлического прыжка (рис. III. 8), когда за стекающей
www.chem21.info
Расход водослива с широким порогом
Для водослива с тонкой стенкой характерно соотношение…
R S/H<0,67
£ 0,67<S/H<2
£ 2<S/H<10
£ S/H<12
493. Задание {{ 1637 }} KT=1 Тема 27-0-0
Укажите, где измеряется глубина потока на водосливе с широким порогом
£ в конце водослива, где происходит искривление линий тока
£ в начальном сечении порога, где наблюдается след кривой свободной поверхности
R в сечении, где давление распределяется по гидростатическому закону в месте перегиба кривой свободной поверхности
494. Задание {{ 1639 }} KT=1 Тема 27-0-0
укажите, какой расход водослива с широким порогом больше: при свободном истечении или при несвободном истечении
R расходы равны
£ при несвободном истечении
£ при свободном истечении
495. Задание {{ 1640 }} KT=1 Тема 27-0-0
Коэффициент расхода водослива с широким порогом опытным путем определяется как…
£ произведение безразмерных коэффициентов сжатия и скорости
R отношение действительного расхода к теоретическому
£ равный коэффициенту скорости, при условии, что коэффициент сжатия струи равен единице
496. Задание {{ 1641 }} KT=1 Тема 27-0-0
Геометрический напор над гребнем водослива с широким порогом при высоте порога больше единицы равен разнице отметок…
R уровня воды в верхнем бьефе и порога водослива
£ уровней воды в верхнем и нижнем бьефах
£ уровня воды и дна подводящего русла в верхнем бьефе
497. Задание {{ 1728 }} КТ=1 Тема 27-0-0
Отметьте правильный ответ
R через водосливы
£ потока жидкости
£ через короткие трубопроводы
£ при равномерном движении воды в канале
498. Задание {{ 1642 }} KT=1 Тема 27-0-0
Геометрический напор на водосливе – это…
£ глубина воды перед водосливом в сечении на расстоянии 3Н, где нет заметного спада свободной поверхности
R превышение над гребнем водосливной стенки уровня воды в верхнем бьефе
£ превышение над гребнем водосливной стенки уровня воды в сечении, где нет заметного спада свободной поверхности
499. Задание {{ 1643 }} KT=1 Тема 27-0-0
Коэффициент расхода водослива с тонкой стенкой опытным путем определяется как…
£ произведение безразмерных коэффициентов сжатия и скорости
R отношение действительного расхода к теоретическому
£ равный коэффициенту скорости, при условии, что коэффициент сжатия струи равен единице
500. Задание {{ 1644 }} KT=1 Тема 27-0-0
Выберите, в каком случае получается подтопленный водослив с тонкой стенкой
R уровень нижнего бьефа располагается выше гребня водослива; в нижнем бьефе имеет место спокойное состояние потока
£ уровень нижнего бьефа располагается выше гребня водослива; в нижнем бьефе имеет место бурное состояние потока
£ уровень нижнего бьефа располагается ниже гребня водослива; в нижнем бьефе имеет место спокойное состояние потока
501. Задание {{ 1645 }} KT=1 Тема 27-0-0
Коэффициент расхода водослива практического профиля полигонального очертания в системе СИ имеет размерность…
R безразмерный
£ м
£ см
£ м3
502. Задание {{ 1646 }} KT=1 Тема 27-0-0
Коэффициент расхода водослива практического профиля криволинейного очертания в системе СИ имеет размерность…
R безразмерный
£ м
£ см
£ м3
503. Задание {{ 1647 }} KT=1 Тема 27-0-0
Укажите при постоянном напоре Н=const какой коэффициент расхода больше: m или mо
£ m> mо
£ m= mо
R mо> m
504. Задание {{ 1648 }} KT=1 Тема 27-0-0
Водослив, у которого давление под струей меньше атмосферного называется…
£ несовершенный
£ с боковым сжатием
£ подтопленный
R совершенный
505. Задание {{ 1649 }} KT=1 Тема 27-0-0
Водослив с тонкой стенкой будет подтоплен при…
£ надвинутом гидравлическом прыжке и Р>hб
£ огогнанном гидравлической прыжке и Р<hб
£ гидравлическом прыжке в предельном положении и Р>==hб
R надвинутом гидравлическом прыжке и Р<hб
506. Задание {{ 1650 }} KT=1 Тема 27-0-0
Выберете основные параметры, от которых зависит расход неподтопленного водослива
£ от длины водосливного фронта b, скорости подхода V0, напора над гребнем Н
£ от длины водосливного фронта b, напора над гребнем Н, ускорения свободного падения g
R от длины водосливного фронта b, скорости подхода V0, напора над гребнем Н, ускорения свободного падения g
507. Задание {{ 1651 }} KT=1 Тема 27-0-0
Истечение через водослив происходит под действием силы…
£ трения
£ поверхностного натяжения
£ трения и поверхностного натяжения
R тяжести
508. Задание {{ 1652 }} KT=1 Тема 27-0-0
Укажите, в чем различие коэффициентов расхода m и mо
R mо учитывает скорость подхода
£ mо не учитывает скорость подхода
£ m учитывает скорость подхода
509. Задание {{ 1653 }} KT=1 Тема 27-0-0
Укажите, какой коэффициент расхода больше m или mо для водослива-водомера Томсона при Н=const
£ m> mо
£ m= mо
R mо> m
510. Задание {{ 1654 }} KT=1 Тема 27-0-0
Перечислите, какие возможны формы струи при истечении через водослив с тонкой стенкой без доступа воздуха под нее
£ поджатая неподтопленная, поджатая подтопленная
£ поджатая неподтопленная, прилипшая
R поджатая неподтопленная, поджатая подтопленная, прилипшая
511. Задание {{ 1655 }} KT=1 Тема 27-0-0
Выберете диапазон, в котором находится значение коэффициента расхода для совершенного водослива с тонкой стенкой
£ 0,409< m0<0,49
£ m0<0,409
R m0>0,49
£ 0,3< m0<0,385
512. Задание {{ 1656 }} KT=1 Тема 27-0-0
Водослив с тонкой стенкой будет подтоплен, если соблюдается условие
£ при отогнанном гидравлическом прыжке и Р<hб
£ при гидравлическом прыжке в предельном положении и Р<hб
£ при надвинутом гидравлической прыжке и Р>hб
R при надвинутом гидравлическом прыжке и Р<hб
513. Задание {{ 1657 }} KT=1 Тема 27-0-0
Выберете значение коэффициента расхода трапецеидального водослива-водомера при Н=(0,05-1,00)м; Р=(3-4)Н и V0<=0,5м/с
£ m0=0,316
£ m=0,625
£ m=0,490
R m0=0,420
514. Задание {{ 1658 }} KT=1 Тема 27-0-0
Коэффициент расхода водослива с тонкой стенкой в системе СИ имеет размерность…
R безразмерный
£ м
£ см
£ м3
515. Задание {{ 1659 }} KT=1 Тема 27-0-0
Для водослива практического профиля характерно соотношение…
£ S/H<0,67
R 0,67<S/H<2
£ 2<S/H<10
£ S/H<12
516. Задание {{ 1660 }} KT=1 Тема 27-0-0
Для водослива с широким порогом характерно соотношение…
£ S/H<0,67
£ 0,67<S/H<2
R 2<S/H<10
£ S/H<12
517. Задание {{ 1661 }} KT=1 Тема 27-0-0
Коэффициент расхода водослива практического профиля криволинейного очертания в системе СИ имеет размерность…
R безразмерный
£ м
£ см
£ м3
518. Задание {{ 1662 }} KT=1 Тема 27-0-0
Коэффициент расхода водослива практического профиля полигонального очертания в системе СИ имеет размерность…
R безразмерный
£ м
£ см
£ м3
519. Задание {{ 1663 }} KT=1 Тема 27-0-0
Соотношение S/H<0,67 обуславливает водослив…
£ с широким порогом
R с тонкой стенкой
£ практического профиля криволинейного очертания
£ практического профиля распластанного типа
520. Задание {{ 1664 }} KT=1 Тема 27-0-0
Укажите силу, под действием которой преимущественно происходит истечение через водослив с тонкой стенкой
£ сила поверхностного натяжения
£ сила инерции
R сила тяжести
£ сила инерции и трения
521. Задание {{ 1665 }} KT=1 Тема 27-0-0
Укажите в чем различие коэффициентов расхода m и m0
£ коэффициент расхода m учитывает скорость подхода
£ коэффициент расхода m0 не учитывает скорость подхода
R коэффициент расхода m0 учитывает скорость подхода
522. Задание {{ 1666 }} KT=1 Тема 27-0-0
Водослив, давление вокруг струи которого атмосферное называется…
£ несовершенный
R совершенный
£ подтопленный
£ с боковым сжатием
523. Задание {{ 1667 }} KT=1 Тема 27-0-0
Укажите расстояние от гребня водослива с тонкой стенкой, на котором определяется отметка уровня воды в верхнем бьефе
£ L=H
£ L<3H
R L>3H
£ L>5H
524. Задание {{ 1668 }} KT=1 Тема 27-0-0
Укажите расстояние, на котором измеряется напор на водосливе
£ L=H
£ L<3H
R L=(3-4)H
fiziku5.ru
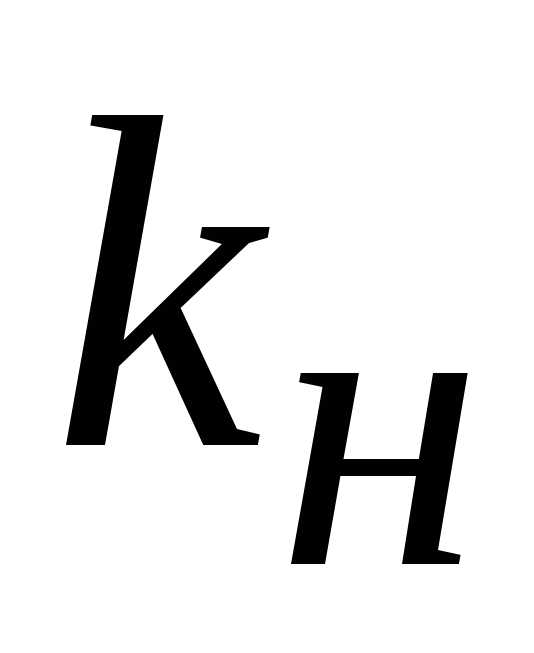 в зависимости от отношения
в зависимости от отношения