Площадь круга | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Для того чтобы найти площадь круга, существует единственная формула, которую нужно запомнить – это произведение числа π на квадрат радиуса.
Доказательством этой формулы будет служить следующий расчет. На чертеже внутри и снаружи круга рисуем правильный многоугольник – многоугольник с равными сторонами.
Из центра круга проводим радиусы в указанные вершины многоугольников. Радиусы во вписанном многоугольнике делят его на определенное количество n одинаковых равнобедренных треугольников. Таким образом, площадь вписанного многоугольника – это n площадей треугольников Sв=nS∆. Тогда как площадь каждого треугольника, исходя из его свойств, равна . Так как конгруэнтные стороны a этого треугольника являются радиусами, то формула приобретает вид , а формула площади всего многоугольника – , считая сумму всех сторон nc, как периметр многоугольника P. Аналогично получаем площадь описанного многоугольника: . Если считать, что количество nc, как сторон многоугольника стремится к бесконечности, то его форма максимально приближается к кругу, и периметр становится близок по значению к длине окружности, а cosα стремится к 1. В этом случае обе формулы – и для вписанного, и для описанного многоугольника приобретают следующий вид:
Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр или длину окружности.
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два. Так как в первоначальной формуле S=πr2 радиус возводится во вторую степень, полученная половина диаметра также должна будет быть в квадрате, и это уже будет выглядеть как .
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель: . Подставляя это в основную формулу, не забываем возвести выражение во вторую степень, и получаем, что площадь круга через длину окружности равна .
geleot.ru
Формула площади круга через диаметр или радиус или длину окружности.
Круг это плоская фигура, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус).
Радиус круга — отрезок, соединяющий центр окружности и любую, максимально удаленную от центра точку круга.
Диаметр круга — отрезок, соединяющий две любые точки максимально удаленные от центра круга и проходящий через этот центр. Диаметр, в два раза больше радиуса
Зная диаметр
или радиус круга или длину окружности, можно найти его площадь.
r — радиус круга
D — диаметр круга
π ≈ 3.14
Формула площади круга, (
Решения задач
на тему: Площадь круга
Калькулятор для расчета площади круга через радиус
Калькулятор для расчета площади круга через диаметр
L — длина окружности
О — центр круга
π ≈ 3.14
Формула площади круга если известна длина окружности, (S):
Решения задач
на тему: Площадь круга
Калькулятор для расчета площади круга через длину
- Подробности
- Автор: Сергей Кондратов
www-formula.ru
Площадь круга — формулы, примеры расчетов
Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность. 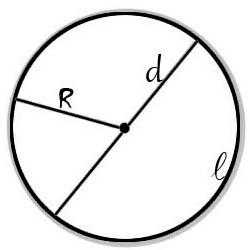
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно: Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности.
Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.Теперь используем данные для примера расчета площади круга по приведенной выше формуле:
Как видим, в результате получаем тот же ответ, что и при первых расчетах.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Итого площадь круга будет равна 5 кв. см.
Площадь круга описанного вокруг квадрата
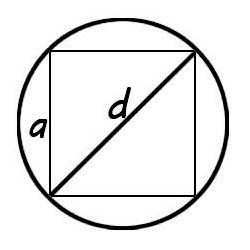
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: отсюда .
После того, как найдем диагональ – мы сможем рассчитать радиус: .
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Задача: дан квадрат, вписанный в круг. Его сторона a = 4 см. Найдите площадь окружности.
Для начала рассчитаем длину диагонали d.
Теперь подставляем данные в формулу
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.
2mb.ru
определить площадь круга, если известна длина окружности
Условие задачи:
Длина окружности 5 м. Найти площадь круга, ограниченного этой окружностью.Дано:
Длина окружности, L = 5 м
Пояснение к рисунку:
O — центр окружности
Найти площадь круга: S
Решение
Используем формулу площади круга через радиус. Но нам пока не известен радиус, его надо найти.
Определить радиус, нам поможет формула длины окружности.
После преобразования, выразим радиус через длину окружности и подставим значения.
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Получили значение радиуса окружности.
В формулу площади круга, подставляем найденное значение радиуса.
Ответ:
Если в формулу площади круга подставить выраженный радиус через длину окружности, то получим следующую формулу, в которой площадь круга сразу выражена через длину окружности. Проверим, подставив наше значение
Калькулятор для расчета площади круга
www-formula.ru
Как найти площадь круга по формулам через диаметр, радиус, длину окружности, расчет площади сектора круга
Как найти площадь круга?
Для того, чтобы рассчитать площадь круга, необходимо знать следующие данные:
- Длину диаметра – отрезка, проходящего через центр круга и соединяющего две противоположные точки окружности, либо радиуса – отрезка, одна из крайних точек которого находится в центре круга, а вторая – на дуге окружности. Таким образом, диаметр равен длине радиуса, умноженной на два.
- Значение числа π. Эта величина представляет собой константу – иррациональную дробь, не имеющую конца. При этом она не является периодической. Данное число выражает соотношение длины окружности к ее радиусу. Для вычисления площади круга в заданиях школьного курса используется значение π, приведенное с точностью до сотых – 3,14.
Формулы для нахождения площади круга, его сегмента или сектора
В зависимости от специфики условий геометрической задачи применяются две формулы нахождения площади круга:
- Если известен радиус r, то расчет производится следующим образом: S= π*r2
- Площадь круга через диаметр d вычисляется другим способом: S = π*d2/ 4
Чтобы определить, как найти площадь круга проще всего, нужно тщательно проанализировать условия задания.
Школьный курс геометрии также включает в себя задачи на расчет площади сегментов или секторов, для которых применяются специальные формулы:
- Сектор представляет собой часть круга, ограниченную окружностью и углом с вершиной, расположенной в центре. Площадь сектора рассчитывается по формуле: S = (π*r
- r – радиус;
- А – величина угла в градусах.
- r – радиус;
- р – длина дуги.
- Сегмент – представляет собой часть, ограниченную сечением круга (хордой) и окружностью. Его площадь можно найти по формуле S=(π*r2/360)*А± S∆;
Также существует второй вариант S = 0,5*р*r;
- r – радиус;
- А – величина угла в градусах;
- S∆ – площадь треугольника, сторонами которого являются радиусы и хорда круга; при этом одна из его вершин располагается в центре круга, а две других – в точках соприкосновения дуги окружности с хордой. Важный момент – знак “минус” ставится в том случае, если значение А меньше 180 градусов, а знак “плюс” – если больше 180 градусов.
Чтобы упростить решение геометрической задачи, можно вычислить площадь круга он-лайн. Специальная программа быстро и безошибочно сделает расчет за пару секунд. Как рассчитать он-лайн площадь фигур? Для этого необходимо известные ввести исходные данные: радиус, диаметр, величину угла.
Структура раздела Справочные материалы:
beta-ege.ru
Формула площади круга
В геометрии кругом называется некоторое множество всех точек на плоскости, которые удалены от одной точки, называемой его центром, на расстояние, не большее заданного, называемого его радиусом. При этом внешней границей круга является окружность, а в том случае, если длина радиуса равна нулю, круг вырождается в точку.
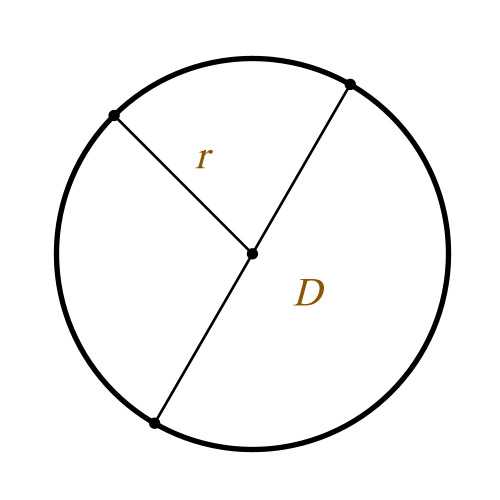
Определение площади круга
При необходимости площадь круга можно вычислить по формуле:
r – радиус круга
D – диаметр круга
S – площадь круга
π – 3.14
Эта геометрическая фигура очень часто встречается как в технике, так и в архитектуре. Конструкторы машин и механизмов разрабатывают различные детали, сечения многих из которых представляют собой именно круг. К примеру, таковыми являются валы, штоки, тяги, цилиндры, оси, поршни и так далее. При изготовлении этих деталей используются заготовки из различных материалов (металлов, древесины, пластических масс), их сечения также представляют собой именно круг. Само собой разумеется, что разработчикам нередко приходится вычислять площадь круга через диаметр или радиус, используя для этой цели несложные математические формулы, открытые еще в глубокой древности.
Именно тогда круглые элементы стали активно и широко использоваться в архитектуре. Один из самых ярки тому примеров – цирк, представляющий собой разновидность строений, предназначенных для проведения в них различных зрелищных мероприятий. Их арены имеют форму круга, а впервые они стали строиться еще во времена античности. Само слово «circus» в переводе с латинского языка означает «круг». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т. д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить площадь круга через диаметр, то получится, что для цирковой арены эта величина составляет 113,04 квадратных метра.
Архитектурными элементами, которые могут принимать форму круга, являются окна. Конечно, в большинстве случаев они прямоугольные или же квадратные (причем во многом благодаря тому, что это проще как для зодчих, так и для строителей), но в некоторых зданиях можно встретить и круглые окна. Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.
Отнюдь не является редкостью использование круглых элементов для производства мебели, например столов и стульев. Существует даже понятие «круглый стол», которое подразумевает конструктивную дискуссию, в ходе которой происходит всестороннее обсуждение различных важных проблем и вырабатывается пути их решения. Что касается изготовления самих столешниц, имеющих круглую форму, то для их производства применяются специализированные инструменты и оборудование, при условии участия рабочих с довольно высокой квалификацией.
simple-math.ru
Как найти площадь, если известен диаметр
Зная лишь длину диаметра окружности, можно вычислить не только площадь круга, но и площади некоторых других геометрических фигур. Это вытекает из того, что диаметры вписанных или описанных вокруг таких фигур окружностей совпадают с длинами их сторон либо диагоналей.Инструкция
- Если надо найти площадь круга (S) по известной длине его диаметра (D), умножайте число пи (π) на возведенную в квадрат длину диаметра, а результат делите на четыре: S=π ²*D²/4. Например, если диаметр круга равен двадцати сантиметрам, то его площадь можно вычислить так: 3,14² * 20² / 4 = 9,86 * 400 / 4 = 986 квадратных сантиметров.
- Если надо найти площадь квадрата (S) по диаметру описанной вокруг него окружности (D), возводите длину диаметра в квадрат, а результат разделите пополам: S=D²/2. Например, если диаметр описанной окружности равен двадцати сантиметрам, то площадь квадрата можно вычислить так: 20² / 2 = 400 / 2 = 200 квадратных сантиметров.
- Если площадь квадрата (S) нужно найти по диаметру вписанной в него окружности (D), достаточно возвести длину диаметра в квадрат: S=D². Например, если диаметр вписанной окружности равен двадцати сантиметрам, то площадь квадрата можно вычислить так: 20² = 400 квадратных сантиметров.
- Если надо найти площадь прямоугольного треугольника (S) по известным диаметрам вписанной (d) и описанной (D) вокруг него окружностей, то возводите длину диаметра вписанной окружности в квадрат и делите на четыре, а к результату прибавляйте половину произведения длин диаметров вписанной и описанной окружностей: S=d²/4 + D*d/2. Например, если диаметр описанной окружности равен двадцати сантиметрам, а вписанной – десяти сантиметрам, то площадь треугольника можно вычислить так: 10² / 4 + 20*10/2 = 25 + 100 = 125 квадратных сантиметров.
- Используйте встроенный в поисковую систему Google калькулятор для проведения необходимых расчетов. Например, чтобы рассчитать с помощью этого поисковика площадь прямоугольного треугольника по данным примера из четвертого шага, надо ввести такой поисковый запрос: «10^2 / 4 + 20*10/2», а затем нажать клавишу Enter.
completerepair.ru