Решение прямоугольного треугольника | Формулы и расчеты онлайн
Решение прямоугольного треугольника по двум сторонам
Если даны две стороны прямоугольного треугольника, то третья сторона может быть вычислена по теореме Пифагора. Острые углы определяются по формулам тригонометрических функций острого угла — Синус угла — sin(A), Косинус угла — cos(A), Тангенс угла — tg(A), Котангенс угла — ctg(A), Секанс угла — sec(A), Косеканс угла — cosec(A).
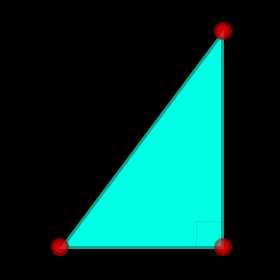
Решение прямоугольного треугольника
Если известны катет a и гипотенуза c
Второй катет b определится по теореме Пифагора:
\[ b = \sqrt{c^2 — a^2} \]
Угол A определится по формуле синуса:
\[ \sin(A) = \frac{a}{c} \]
Поскольку сумма всех углов треугольника равна 180° то второй острый угол определится так:
\[ B = 180° — 90° — A \]
Вычислить, найти решение прямоугольного треугольника по двум сторонам (катет и гипотенуза)
Если известны катеты a и b
Гипотенуза с определится по теореме Пифагора:
\[ c = \sqrt{a^2 + b^2} \]
Угол A определится по формуле тангенса:
\[ \tg(A) = \frac{a}{b} \]
Поскольку сумма всех углов треугольника равна 180° то второй острый угол определится так:
\[ B = 180° — 90° — A \]
Вычислить, найти решение прямоугольного треугольника по двум сторонам (катет и катет)
Решение прямоугольного треугольника по стороне и острому углу
Если дан острый угол A, то B найдется по формуле:
\[ B = 90° — A \]
Стороны можно найти по следующим формулам:
\[ a = c · \sin(A) \] | \[ b = c · \cos(A) \] | \[ a = b · \tg(A) \] |
\[ b = c · \sin(B) \] | \[ a = c · \cos(B) \] | \[ b = a · \tg(B) \] |
\[ c = \frac{a}{\sin(A)} \] | \[ c = \frac{b}{\cos(A)} \] | \[ b = \frac{a}{\tg(A)} \] |
Вычислить, найти решение прямоугольного треугольника если известны катет a и противолежащий угол A
Здесь все углы мы найдем по формуле (7). Гипотенузу по формуле (14) и второй катет по формуле (16).
В помощь студенту
Решение прямоугольного треугольника |
стр. 237 |
|---|
Два угла и сторона треугольника C
Для того чтобы рассчитать в треугольнике все возможные показатели, необходимо, как минимум, иметь данные о его сторонах. Зная два угла и сторону а, можно найти остальные две стороны и угол, построив высоту в таком треугольнике. (рис. 76.1) Высота разделит произвольный треугольник на два прямоугольных, в которых катетами будет высота и часть известной стороны x или y, а гипотенузами – неизвестные стороны a и b. Кроме того, что мы задаем известную сторону a, как сумму двух катетов x и y, тригонометрия полученных треугольников, определяет высоту с одной стороны как произведение y на тангенс β, а с другой стороны как произведение x на тангенс γ. Приравнивая эти выражения друг к другу, можно составить систему уравнений, из которых могут быть найдены части x и y, а затем неизвестные стороны первоначального треугольника a и b. {█(x+y=a@y tanβ=x tanγ )┤{█(x=a-y@y(tanβ+tanγ )=a tanγ )┤{█(x=a-y@y=(a tanγ)/(tanβ+tanγ ))┤ b=x/cosγ , c=y/cosβ h_a=y tanβ
Можно также найти сразу две другие высоты треугольника, опущенные на стороны b и c соответственно. (рис. 76.2) h_b=a sinβ h_c=a sinγ
Третий угол можно найти, зная, что сумма всех углов в треугольнике равна 180 градусам. α=180°-β-γ
Теперь, зная все стороны, углы и высоты, можно найти все остальные параметры треугольника. Вычислить периметр можно, сложив все три стороны, а площадь – умножив половину любой стороны на опущенную на нее высоту. P=a+b+c S=(ah_a)/2
Если провести в треугольнике медианы, то каждая из них разделит сторону, на которую она опущена, на две равные части. Для того, чтобы вычислить медиану в треугольнике, необходимо знать все три стороны. Формула медианы заключается в том, чтобы сложить удвоенные квадраты двух нетронутых сторон, отнять квадрат стороны, на которую опущена медиана, извлечь из этого выражения квадратный корень и разделить его на два. (рис. 75.1) m_c=√(2a^2+2b^2-c^2 )/2 m_a=√(2b^2+2c^2-a^2 )/2 m_b=√(2a^2+2c^2-b^2 )/2
Чтобы найти биссектрисы треугольника, которые делят пополам его углы, также необходимо знать все три стороны треугольника. Формула биссектрисы выглядит немного сложнее, чем формула медианы, но достаточно проста в расчетах. (рис.75.2) l_c=√(ab(a+b+c)(a+b-c))/(a+b) l_b=√(ac(a+b+c)(a+c-b))/(a+c) l_a=√(bc(a+b+c)(b+c-a))/(b+c)
Средняя линия треугольника – это прямая, проведенная параллельно одной из его сторон. Ее особенность заключается в том, что она делит стороны на которые опирается на две равные части, и сама равна половине стороны, ей параллельной. (рис.75.7) M_a=a/2 M_b=b/2 M_c=c/2
Также в произвольном треугольнике через стороны можно найти радиус окружности, которую можно вписать в треугольник или описать около него. Радиус вписанной окружности будет начинаться в точке пересечения биссектрис треугольника и опускаться на любую из сторон под прямым углом. Радиус описанной окружности начинается в точке пересечения медиатрисс треугольника и заканчивается в любой из его вершин. (рис. 75.5, 75.6) r=√(((p-a)(p-b)(p-c))/p) R=abc/(4√(p(p-a)(p-b)(p-c)))
geleot.ru
Расчет углов правильного многоугольника онлайн
Многоугольник представляет плоскую замкнутую геометрическую фигуру, у которой может быть три, четыре и более сторон, пересекающихся в трех, четырех и более точках, называющихся вершинами. Называются они в соответствии с количеством сторон или вершин. Например, многоугольник с пятью сторонами называется пятиугольник, с шестью — шестиугольник и т. д. Правильным называют многоугольник с равными углами и сторонами. Например, квадрат. Если в задании известна одна из этих величин, несложно узнать остальные. В равностороннем n-угольнике, сумма всех углов рассчитывается как:
(n — 2) 180°
а сумма всех его сторон будет равна:
P = na
P — периметр;
а — сторона;
n — количество сторон.
Определяем угол правильного n-угольника:
А = (n — 2) / n х 180°
Если в задании имеется радиус вписанной окружности ®, тогда сторону (а) правильного n-угольника определяет по формуле:
a = 2r · tg · 180° / n
a = 2r · tg · π / n
Если задан радиус ® описанной окружности, то находим сторону по формуле:
a = 2 R · sin · 180° / n
a = 2 R · sin · π / n
Соответственно, если известна сторона правильного n-угольника, находим r вписанной окружности:
r = a / (2 tg · 180° / n)
r = a / (2 tg · π / n)
и R описанной окружности n-угольника по его стороне:
R= a / (2 sin · 180° / n)
R= a / (2 sin · π / n)
Онлайн калькулятор поможет вам быстро и правильно определить число и величину сторон правильного многоугольника, размер его внешнего и внутреннего углов, а также другие показатели.Расчет углов правильного многоугольника
infofaq.ru
Онлайн калькулятор: Тригонометрические функции
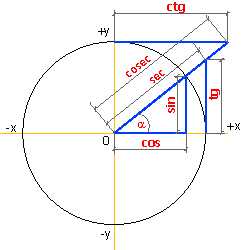Простейшие тригонометрические функцииТригонометрические функции — вид элементарных функций, к которым относятся следующие функции:
sin — синус
cos — косинус
tg — тангенс
ctg — котангенс
sec — секанс
cosec — косеканс
versin — версинус (синус-верзус)
vercos — коверсинус (косинус-верзус)
exsec — экссеканс
excsc — экскосеканс
Для того чтобы вычислить все эти тригонометрические функции сразу для заданного угла, введите значение угла в поле Угол и получите результат в виде таблицы значений всех функций для этого угла. Угол можно задать в градусах, радианах, градах, минутах и секундах, для выбора единицы измерения — просто щелкните на ее название.
Тригонометрические функции
Единицы измерения Точность вычисленияЗнаков после запятой: 10
save Сохранить share Поделиться extension Виджет
Как известно из школы, синус угла (sin) — это отношение длины противоположного этому углу катета к гипотенузе, а косинус (cos) — это отношение прилежащего этому углу катета к гипотенузе.
Остальные тригонометрические функции можно выразить через синус и косинус:
Тангенс: (отношение длины противоположного углу катета к прилежащему катету)
Секанс: (отношение длины гипотенузы к прилежащему к углу катету)
Косеканс: (отношение длины гипотенузы к противоположному катету)
Редко используемые тригонометрические функции:
Версинус:
Коверсинус:
Гаверсинус:
Экссеканс:
Экскосеканс:
planetcalc.ru