Чтобы найти площадь что нужно сделать чтобы – Какие измерения надо провести,чтобы найти площадь прямоугольника?, русский язык

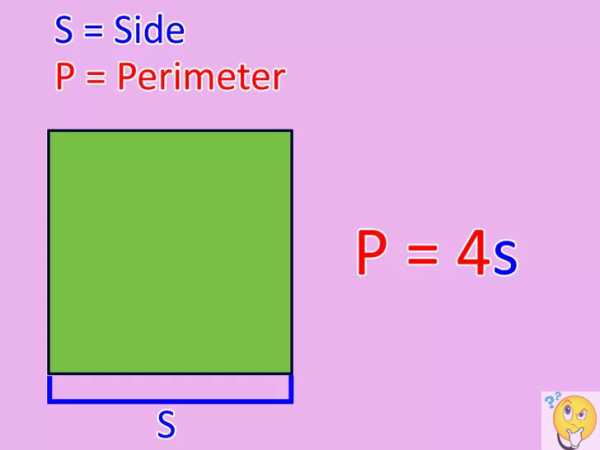
Как найти площадь прямоугольника

С таким понятием, как площадь, нам приходится сталкиваться в своей жизни повседневно. Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем жизненном пути встает очень часто и является важным не только для школьников.

Для тех, кто не знает, прямоугольник – это плоская фигура, у которой противоположные стороны равны, а углы составляют 90о. Для обозначения площади в математике используют английскую букву S. Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.

Теперь попытаемся дать подробный ответ на вопрос, как найти площадь прямоугольника. Существует несколько способов определения этой величины. Наиболее часто мы сталкиваемся со способом определения площади с помощью ширины и длины.

Возьмем прямоугольник с шириной b и длиной k. Для вычисления площади данного прямоугольника необходимо ширину умножить на длину. Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k.

А теперь рассмотрим этот способ на конкретном примере. Необходимо определить площадь садового участка с шириной 2 метра и длиной 7 метров.

S = 2 * 7 = 14 м2

В математике, особенно в старших классах, приходится определять площадь иными способами, так как во многих случаях ни длина, ни ширина прямоугольника нам не известна. Вместе с тем имеют место другие известные величины. Как найти площадь прямоугольника в этом случае?

• Если нам известна длина диагонали и один из углов, составляющий диагональ с любой стороной прямоугольника, то в этом случае потребуется вспомнить о площади прямоугольного треугольника. Ведь если разобраться, то прямоугольник состоит из двух равных прямоугольных треугольников. Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника. Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.

В виде формулы это будет выглядеть так:

S = cos(a) * sin(a) * d2 , где d- длина диагонали

• Еще один способ определения площади прямоугольника – через вписанную в него окружность. Он применяется в том случае, если прямоугольник является квадратом. Для использования данного способа необходимо знать радиус окружности. Как вычислить площадь прямоугольника таким способом? Конечно же, по формуле. Доказывать мы ее не будем. А выглядит она так: S = 4 * r2, где r –радиус.

Случается так, что вместо радиуса нам известен диаметр вписанной окружности. Тогда формула будет выглядеть так:

S=d2,где d – диаметр.

• Если известна одна из сторон и периметр, то как узнать площадь прямоугольника в этом случае? Для этого необходимо произвести ряд простых вычислений. Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:

S=b* (P – 2*b), где b – длина стороны, P – периметр.

Как видим площадь прямоугольника можно определять различными способами. Все зависит от того, какие величины нам известны перед рассмотрением данного вопроса. Конечно же, последние методы исчисления в жизни практически не встречаются, но могут пригодиться для решений многих задач в школе. Возможно, и для решения ваших задач эта статья окажется полезной.

fb.ru

Как посчитать площадь прямоугольника: практические советы

Одна из первых формул, которая изучается в математике, связана с тем, как посчитать площадь прямоугольника. Она же является и самой часто используемой. Прямоугольные поверхности окружают нас повсюду, поэтому часто требуется знать их площади. Хотя бы для того, чтобы узнать, хватит ли имеющейся в наличии краски для покраски полов.

Какие единицы измерения площади существуют?

Если говорить о той, которая принята за международную, то это будет квадратный метр. Его удобно использовать при расчете площадей стен, потолка или пола. В них указывается площадь жилья.

Когда речь идет о меньших предметах, то вводят квадратные дециметры, сантиметры или миллиметры. Последние нужны, если фигура не больше ногтя.

При измерении площади города или страны самыми подходящими оказываются квадратные километры. Но есть еще и единицы, которые используют для того, чтобы указать размер площади: ар и гектар. Первая из них еще называется соткой.

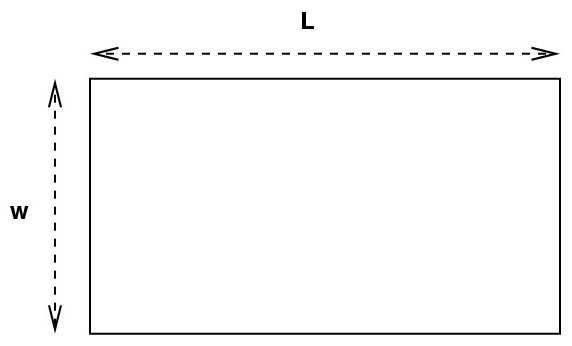
Как быть, если заданы стороны прямоугольника?

Это самый простой способ того, как посчитать площадь прямоугольника. Достаточно просто перемножить обе известные величины: длину и ширину. Формула выглядит так: S = а * в. Здесь буквами а и в обозначены длина и ширина.

Подобным образом рассчитывается площадь квадрата, который является частным случаем прямоугольника. Так как у него все стороны равны, то произведение становится квадратом буквы а.

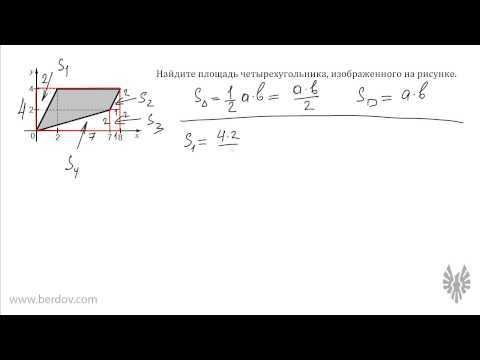
Как быть, если фигура изображена на клетчатой бумаге?

В этой ситуации нужно полагаться на количество клеточек внутри фигуры. По их числу бывает просто посчитать площадь прямоугольника. Но это можно сделать тогда, когда стороны прямоугольника совпадают с линиями клеток.

Часто имеет место такое положение прямоугольника, при котором его стороны наклонены по отношению к разлиновке бумаги. Тогда количество клеток определить сложно, поэтому расчет площади прямоугольника усложняется.

Потребуется сначала узнать площадь прямоугольника, который можно прочертить по клеточкам точно вокруг данного. Это просто: перемножить высоту и ширину. Потом вычесть из получившегося значения площади всех прямоугольных треугольников. А их четыре. К слову, их рассчитывают как половину произведения катетов.

Итоговый результат даст значение площади данного прямоугольника.

Как поступить, если стороны неизвестны, зато даны его диагональ и угол между диагоналями?

До того как находить площадь прямоугольника, в этой ситуации нужно вычислить его стороны, чтобы воспользоваться уже знакомой формулой. Поначалу потребуется вспомнить свойство его диагоналей. Они равны и делятся точкой пересечения пополам. Можно увидеть на чертеже, что диагонали делят прямоугольник на четыре равнобедренных треугольника, которые попарно равны друг другу.

Равные стороны этих треугольников определяются как половины диагонали, которая известна. То есть в каждом треугольнике есть две стороны и угол между ними, которые даны в задаче. Можно воспользоваться теоремой косинусов.

Одна сторона прямоугольника будет вычислена по формуле, в которой фигурируют равные стороны треугольника и косинус заданного угла. Для вычисления второй значение косинуса придется брать от угла, равного разности 180 и известного угла.

Теперь задача о том, как посчитать площадь прямоугольника, сводится к простому перемножению двух полученных сторон.

Что делать, если в задаче дан периметр?

Обычно в условии указывается еще и соотношение длины и ширины. Вопрос о том, как посчитать площадь прямоугольника, в этом случае проще на конкретном примере.

Допустим, что в задаче периметр некоторого прямоугольника равен 40 см. Известно также, что его длина в полтора раза больше ширины. Необходимо узнать его площадь.

Решение задачи начинается с записи формулы периметра. Его удобнее расписать как сумму длины и ширины, каждую из которых умножить на два по отдельности. Это будет первым уравнением в системе, которую потребуется решить.

Второе связано с известным по условию соотношением сторон. Первая сторона, то есть длина, равна произведению второй (ширины) и числа 1,5. Это равенство нужно подставить в формулу для периметра.

Получится, что он равен сумме двух одночленов. Первый — произведение 2 и неизвестной ширины, второй — произведение чисел 2 и 1,5 и той же ширины. В этом уравнении всего одна неизвестная — это ширина. Нужно ее сосчитать, а потом воспользоваться вторым равенством, чтобы сосчитать длину. Останется только перемножить эти два числа, чтобы узнать площадь прямоугольника.

Расчеты дают такие величины: ширина — 8 см, длина — 12 см, а площадь — 96 см². Последнее число — ответ рассмотренной задачи.

fb.ru

Как вычислить площадь прямоугольника?

Одним из важнейших правил тригонометрии является вычисление площади различных фигур, поэтому многие задумываются над тем, как вычислить площадь прямоугольника.

Стоит отметить, что, зная разнообразные величины: стороны, диагонали, углы и периметр фигуры, — можно вычислить ее площадь.

Площадь по двум сторонам

В задаче необходимо найти площадь прямоугольника, если известны две стороны: одна сторона равна 3 см, а другая — 2 см.

Решение:

Исходя из формулы площади S=a*b, мы получаем, что площадь прямоугольника в данном случае равняется:

Ответ: S = 6 см²

Площадь прямоугольника с известной стороной и диагональю

Чтобы решить задачи с такими условиями, необходимо вспомнить теорему Пифагора.

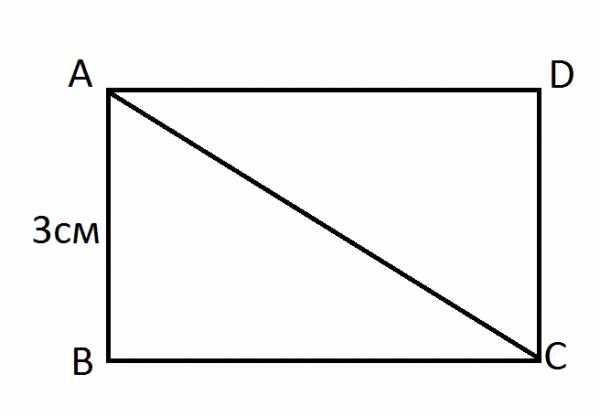
Например, в задаче необходимо найти площадь прямоугольника ABCD, когда известно, что сторона прямоугольника АВ = 3 см, а прилегающая диагональ АС = 5 см.

Решение:

Для начала необходимо узнать вторую сторону прямоугольника. Для этого следует воспользоваться теоремой Пифагора: а² + b² = c². Исходя из теоремы, мы получаем, что сторону ВС можно вычислить следующим способом:

• ВС²= АС²-АВ² = (25-9) = 16 см.
• ВС=4 см.

Таким образом, можно определить и искомое значение:

Ответ: S = 12 см²

О нахождении диагонали прямоугольника можно прочитать в статье Как найти диагональ прямоугольника.

Площадь по диагонали и углу

В задаче необходимо найти площадь прямоугольника, если диагональ равна 10 см, а угол прилегания диагонали к ширине прямоугольника равен 60 градусов.

Решение:

Так как угол между одной стороной и диагональю равен 60 градусам, то прямоугольник делится на два треугольника. Используя формулу S=1/2 d

2*sin α, определяем:

• S= 1/2*10²*sin60°= 50*(√ 3)/2 см² = 25*(√ 3) см²

От

elhow.ru

Площадь прямоугольника онлайн калькулятор

Чему равна площадь прямоугольника? 1. Необходимо знать длину и ширину прямоугольника. 2. Внесите значения сторон в графы ниже. 3. Нажмите кнопку рассчитать площадь прямоугольника!

Прямоугольник — это простая двухмерная геометрическая фигура. Все углы у него прямые, по этому он и называется прямоугольник. Стороны имеют разный размер, попарно, и обычно называются ширина и длина.

Формула площади прямоугольника — посчитать!

L * H = S чтобы найти площадь прямоугольника, необходимо перемножить ширину на длину. Другими словами её можно выразить так: площадь прямоугольника равна произведению сторон.

1. Приведём пример расчёта как найти площадь прямоугольника

, стороны равны известным величинам, например ширина 4 см, длина 8 см.

Как найти площадь прямоугольника со сторонами 4 и 8 см: Решение простое! 4 х 8 = 32 см2. Чтобы решить такую простую задачу нужно вычислить произведение сторон прямоугольника или просто умножить ширину на длину, это и будет площадь!

2. Частным случаем прямоугольника является квадрат, это тот случай когда стороны у прямоугольника равны, в этом случае найти площадь квадрата можно по выше приведённой формуле.

Чему равна площадь прямоугольника?

Умение рассчитывать площадь прямоугольника является базовым навыком для решения огромного количества бытовых или технических задач. Эти знания применяются практически во всех областях жизни! Например в тех случаях когда необходимы площади любых поверхностей в строительстве или недвижимости. При расчётах площадей земли, участков, стен домов, жилых помещений … не возможно назвать ни одной области деятельности человека, где это знание не может пригодиться!

Если расчёт площади прямоугольника вызывает у Вас сложности — просто воспользуйтесь нашим калькулятором! О моментально приведёт все необходимые вычисления и напишет текст решения с разъяснениями в деталях.

allcalculators.ru

Как найти площадь фигуры?

Как найти площадь фигуры?

Знать и уметь рассчитывать площади различных фигур необходимо не только для решения простых геометрических задач. Не обойтись без этих знаний и при составлении или проверке смет на ремонт помещений, расчета количества необходимых расходных материалов. Поэтому давайте разберемся, как находить площади разных фигур.

Площадь

Часть плоскости, заключенная внутри замкнутого контура, называется площадью этой плоскости. Выражается площадь количеством заключенных в ней квадратных единиц.

Чтобы вычислить площадь основных геометрических фигур, необходимо использовать правильную формулу.

Площадь треугольника

Обозначения:

• S — искомая площадь,
• a, b, c — длины сторон треугольника,
• h — высота искомого треугольника,
• γ — угол, находящийся между стороной a и стороной b,
• r — радиус окружности (вписанной в треугольник),
• R — радиус окружности (описанной вокруг треугольника),
• p — половина периметра треугольника.

1. Если известны h, a, то площадь искомого треугольника определяется как произведение длин стороны и высоты треугольника, опущенной к этой стороне, разделенное пополам: S=(a·h)/2
2. Ес

elhow.ru

Площадь прямоугольника — формул, пример расчет, калькулятор

Прямоугольник – это параллелограмм, у которого все углы равны 90°, а противоположные стороны попарно параллельны и равны.

У прямоугольника есть несколько неопровержимых свойств, которые применяются в решении множества задач, в формулах площади прямоугольника и его периметра. Вот они:

• Стороны прямоугольника являются его высотами;
• Длины диагоналей равны между собой ;
• Точка пересечения диагоналей делит их пополам;

Длина неизвестной стороны или диагонали прямоугольника вычисляется по формуле площади прямоугольного треугольника или по теореме Пифагора. Площадь прямоугольника можно найти двумя способами – по произведению его сторон или по формуле площади прямоугольника через диагональ. Первая и самая простая формула выглядит так:

Пример расчета площади прямоугольника по этой формуле очень прост. Зная две стороны, к примеру a =3 см, b = 5 см, мы легко высчитаем площадь прямоугольника:
Получаем, что в таком прямоугольнике площадь будет равна 15 кв. см.

Площадь прямоугольника через диагонали

Иногда требуется применить формулу площади прямоугольника через диагонали. Для нее потребуется не только узнать длину диагоналей, но и угол между ними:

Рассмотрим пример расчета площади прямоугольника через диагонали. Пусть дан прямоугольник с диагональю d = 6 см и углом = 30°. Подставляем данные в уже известную формулу:

Итак, пример расчета площади прямоугольника через диагональ показал нам, что найти площадь таким образом, если задан угол, довольно просто.
Рассмотрим еще одну интересную задачку, которая поможет нам немного размять мозги.

Задача: Дан квадрат. Его площадь равна 36 кв. см. Найдите периметр прямоугольника, у которого длина одной из сторон равна 9 см, а площадь такая же, как у заданного выше квадрата.
Итак, у нас есть несколько условий. Для наглядности запишем их, чтобы увидеть все известные и неизвестные параметры:
Стороны фигуры попарно параллельны и равны. Поэтому периметр фигуры равен удвоенной сумме длин сторон:
Из формулы площади прямоугольника, которая равняется произведению двух сторон фигуры, найдем длину стороны b
Отсюда:
Подставляем известные данные и находим длину стороны b:
Рассчитываем периметр фигуры:
Вот так, зная несколько легких формул, можно вычислить периметр прямоугольника, зная его площадь.

2mb.ru

Как найти площадь квадрата

Для вычисления площади и периметра квадрата нужно разобраться в понятиях этих величин. Квадрат представляет собой прямоугольник только с четырьмя одинаковыми сторонам, которые имеют между собой угол в 90°. Периметр — это сумма длин всех сторон. Площадь — это произведение длины прямоугольной фигуры на ее ширину.

Площадь квадрата и как ее найти

Как было сказано выше, квадрат — это прямоугольник, имеющий 4 равные стороны, поэтому ответом на вопрос: «как найти площадь квадрата» является формула: S = a*a или S = a2, где а — сторона квадрата. Исходя из этой формулы, легко находится сторона квадрата, если известна площадь. Для этого необходимо извлечь квадрат из указанной величины.

Например, S = 121, следовательно, а = √121 = 11. Если заданное значение отсутствует в таблице квадратов, то можно воспользоваться калькулятором: S = 94, а = √94 = 9,7.

Как найти периметр квадрата

Периметр квадрата находится по легкой формуле: Р = 4а, где а — сторона квадрата.

Пример:

• сторона квадрата = 5, следовательно, P = 4*5 = 20
• сторона квадрата = 3, следовательно, Р = 4*3 = 12

Но существуют такие задачи, где заведомо обозначена площадь, а нужно найти периметр. При решении нужны формулы, которые представлены ранее.

Например: как найти периметр квадрата, если известна площадь, равная 144?

Шаги решения:

1. Выясняем длину одной стороны: а = √144 = 12
2. Находим периметр: Р = 4*12 = 48.

Нахождение периметра вписанного квадрата

Существуют еще несколько способов нахождения периметра квадрата. Рассмотрим один из них: нахождение периметра через радиус описанной окружности. Здесь появляется новый термин «вписанный квадрат» — это квадрат, чьи вершины лежат на окружности.

Алгоритм решения:

1. Здесь важно помнить, что отрезок от центра описанной окружности до одной из вершин квадрата является радиусом, поэтому чтобы вычислить периметр фигуры, нужно найти одну из четырех сторон. Условно квадрат делится на два прямоугольных треугольника, которые имеют равные катеты а и b. Их общая гипотенуза с равна радиусу, умноженному на 2, описанной — 2r.
2. Далее стоит обратиться к теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов, т. е. a2 + b2 = c2.

• так как на рассмотрении квадрат, формулу можно выразить таким образом: a2 + a2 = (2r)2;
• затем следует уравнение сделать проще: 2a2 = 4(r)2;
• делим уравнение на 2: (a2) = 2(r)2;
• извлекаем корень: a = √(2r).

В итоге получаем последнюю формулу: а (сторона квадрата) = √(2r).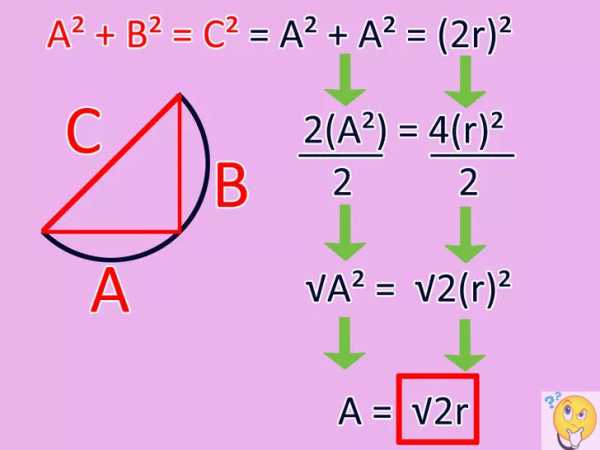

3. Найденная сторона квадрата умножается на 4, далее применяется стандартная формула по нахождению периметра: P = 4√(2r).

Задача:

Дан квадрат, который вписан в окружность, ее радиус равен 5. Значит, диагональ квадрата равняется 10. Применяем теорему Пифагора: 2(a2) = 102, то есть 2a2 = 100. Делим полученное на два и в результате: a2 = 50. Так как это не табличное значение, используем калькулятор: а = √50 = 7,07. Умножаем на 4: Р = 4*7,07 = 28,2. Задача решена!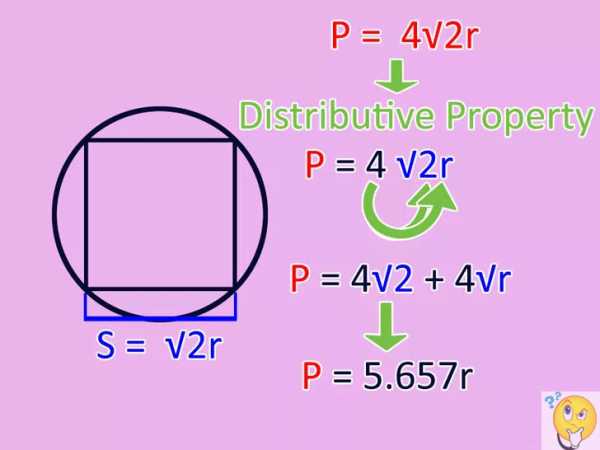

Рассмотрим еще один вопрос

Часто в задачах встречается другое условие: как найти площадь квадрата, если известен периметр?

Мы уже рассмотрели все необходимые формулы, поэтому для решения задач подобного типа, необходимо умело их применять и связывать между собой. Перейдем сразу к наглядному примеру: Площадь квадрата равна 25 см2, найдите его периметр.

Шаги решения:

1. Находим сторону квадрата: а = √25 = 5.

2. Находим сам периметр: Р = 4*а = 4*5 = 20.

Подводя итог, важно напомнить, что такие легкие формулы применимы не только в учебной деятельности, но и повседневной жизни. Периметр и площадь фигуры дети учатся находить еще в начальной школе. В средних классах появляется новый предмет — геометрия, где теорема Пифагора находится в самом начале изучения. Эти азы математики проверяются и по окончанию школы ОГЭ и ЕГЭ, поэтому важно знать эти формулы и правильно их применять.

Похожие статьи

kak-za4em.ru